structure learning view markdown

introduction

  1. structured prediction - have multiple independent output variables
    • output assignments are evaluated jointly
    • requires joint (global) inference
    • can’t use classifier because output space is combinatorially large
    • three steps
    1. model - pick a model
    2. learning = training
    3. inference = testing
  2. representation learning - picking features
    • usually use domain knowledge
  3. combinatorial - ex. map words to higher dimensions
  4. hierarchical - ex. first layers of CNN

structure

  • structured output can be represented as a graph
  • outputs y
  • inputs x
  • two types of info are useful
    • relationships between x and y
    • relationships betwen y and y
  • complexities
    1. modeling - how to model?
    2. train - can’t train separate weight vector for each inference outcome
    3. inference - can’t enumerate all possible structures
  • need to score nodes and edges
    • could score nodes and edges independently
    • could score each node and its edges together

sequential models

sequence models

  • goal: learn distribution $P(x_1,…,x_n)$ for sequences $x_1,…,x_n$
    • ex. text generation
  • discrete Markov model
    • $P(x_1,…,x_n) = \prod_i P(x_i \vert x_{i-1})$
    • requires
      1. initial probabilites
      2. transition matrix
  • mth order Markov model - keeps history of previous m states
  • each state is an observation

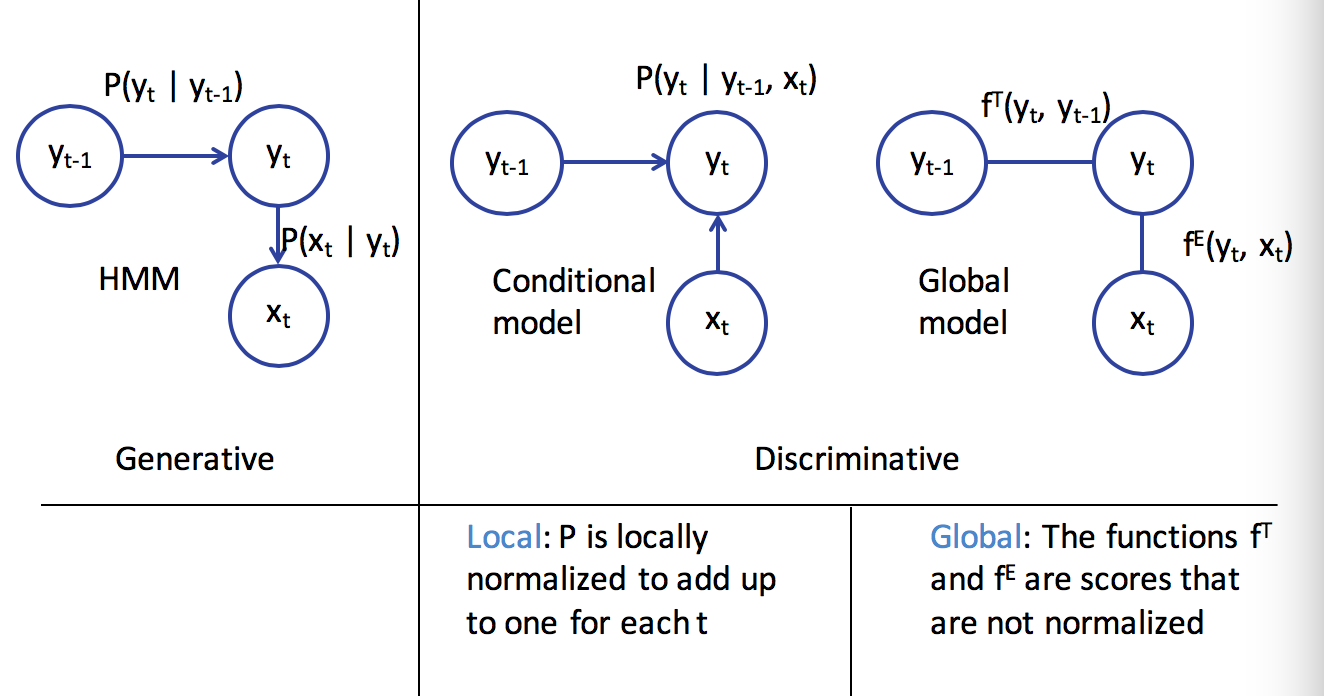
conditional models and local classifiers - discriminative model

  • conditional models = discriminative models
    • goal: model $P(Y\vert X)$
    • learns the decision boundary only
    • ignores how data is generated (like generative models)
  • ex. log-linear models
    • $P(\mathbf{y\vert x,w}) = \frac{exp(w^T \phi (x,y))}{\sum_y’ exp(w^T \phi (x,y’))}$
    • training: $w = \underset{w}{argmin} \sum log : P(y_i\vert x_i,w)$
  • ex. next-state model
    • $P(\mathbf{y}\vert \mathbf{x})=\prod_i P(y_i\vert y_{i-1},x_i)$
  • ex. maximum entropy markov model
    • $P(y_i\vert y_{i-1},x) \propto exp( w^T \phi(x,i,y_i,y_{i-1}))$
      • adds more things into the feature representation than HMM via $\phi$
    • has label bias problem
      • if state has fewer next states they get high probability
        • effectively ignores x if $P(y_i\vert y_{i-1})$ is too high
  • ex. conditional random fields=CRF
    • a global, undirected graphical model
      • divide into factors
    • $P(Y\vert x) = \frac{1}{Z} \prod_i exp(w^T \phi (x,y_i,y_{i-1}))$
      • $Z = \sum_{\hat{y}} \prod_i exp(w^T \phi (x,\hat{y_i},\hat{y}_{i-1}))$
      • $\phi (x,y) = \sum_i \phi (x,y_i,y_{i-1})$
    • prediction via Viterbi (with sum instead of product)
    • training
      • maximize log-likelihood $\underset{W}{max} -\frac{\lambda}{2} w^T w + \sum log : P(y_I\vert x_I,w)$
      • requires inference
    • linear-chain CRF - only looks at current and previous labels
  • ex. structured perceptron
    • HMM is a linear classifier

constrained conditional models

consistency of outputs and the value of inference

  • ex. POS tagging - sentence shouldn’t have more than 1 verb
  • inference
    • a global decision comprising of multiple local decisions and their inter-dependencies
      1. local classifiers
      2. constraints

  • learning

    • global - learn with inference (computationally difficult)

hard constraints and integer programs

soft constraints

inference

  • inference constructs the output given the model

  • goal: find highest scoring state sequence

    • $argmax_y : score(y) = argmax_y w^T \phi(x,y)$
  • naive: score all and pick max - terribly slow
  • viterbi - decompose scores over edges
  • questions
    1. exact v. approximate inference
      • exact - search, DP, ILP
      • approximate = heuristic - Gibbs sampling, belief propagation, beam search, linear programming relaxations
    2. randomized v. deterministic
      • if run twice, do you get same answer
  • ILP - integer linear programs
    • combinatorial problems can be written as integer linear programs
    • many commercial solvers and specialized solvers
    • NP-hard in general
    • special case of linear programming - minimizing/maximizing a linear objective function subject to a finite number of linear constraints (equality or inequality)
      • in general, $ c = \underset{c}{argmax}: c^Tx $ subject to $Ax \leq b$
      • maybe more constraints like $x \geq 0$
      • the constraint matrix defines a polytype
      • only the vertices or faces of the polytope can be solutions
      • $\implies$ can be solved in polynomial time
    • in ILP, each $x_i$ is an integer
    • LP-relaxation - drop the integer constraints and hope for the best
    • 0-1 ILP - $\mathbf{x} \in {0,1}^n$
    • decision variables for each label $z_A = 1$ if output=A, 0 otherwise
    • don’t solve multiclass classification with an ILP solver (makes it harder)
  • belief propagation
    • variable elimination
      1. fix an ordering of the variables
      2. iteratively, find the best value given previous neighbors
        • use DP
        • ex. Viterbi is max-product variable elimination
    • when there are loops, require approximate solution
      • uses message passing to determine marginal probabilities of each variable
        • message $m_{ij}(x_j)$ high means node i believes $P(x_j)$ is high
      • use beam search - keep size-limited priority queue of states

learning protocols

structural svm

  • $\underset{w}{min} : \frac{1}{2} w^T w + C \sum_i \underset{y}{max} (w^T \phi (x_i,y)+ \Delta(y,y_i) - w^T \phi(x_i,y_i) )$

empirical risk minimization

  • subgradients
    • ex. $f(x) = max ( f_1(x), f_2(x))$, solve the max then compute gradient of whichever function is argmax

sgd for structural svm

  • highest scoring assignment to some of the output random variables for a given input?
  • loss-augmented inference - which structure most violates the margin for a given scoring function?
  • adagrad - frequently updated features should get smaller learning rates