Some papers on learning disentangled representations with VAEs, GANs, and other methods.

VAEs

Some good disentangled VAE implementations are here and more general VAE implementations are here. Tensorflow implementations available here

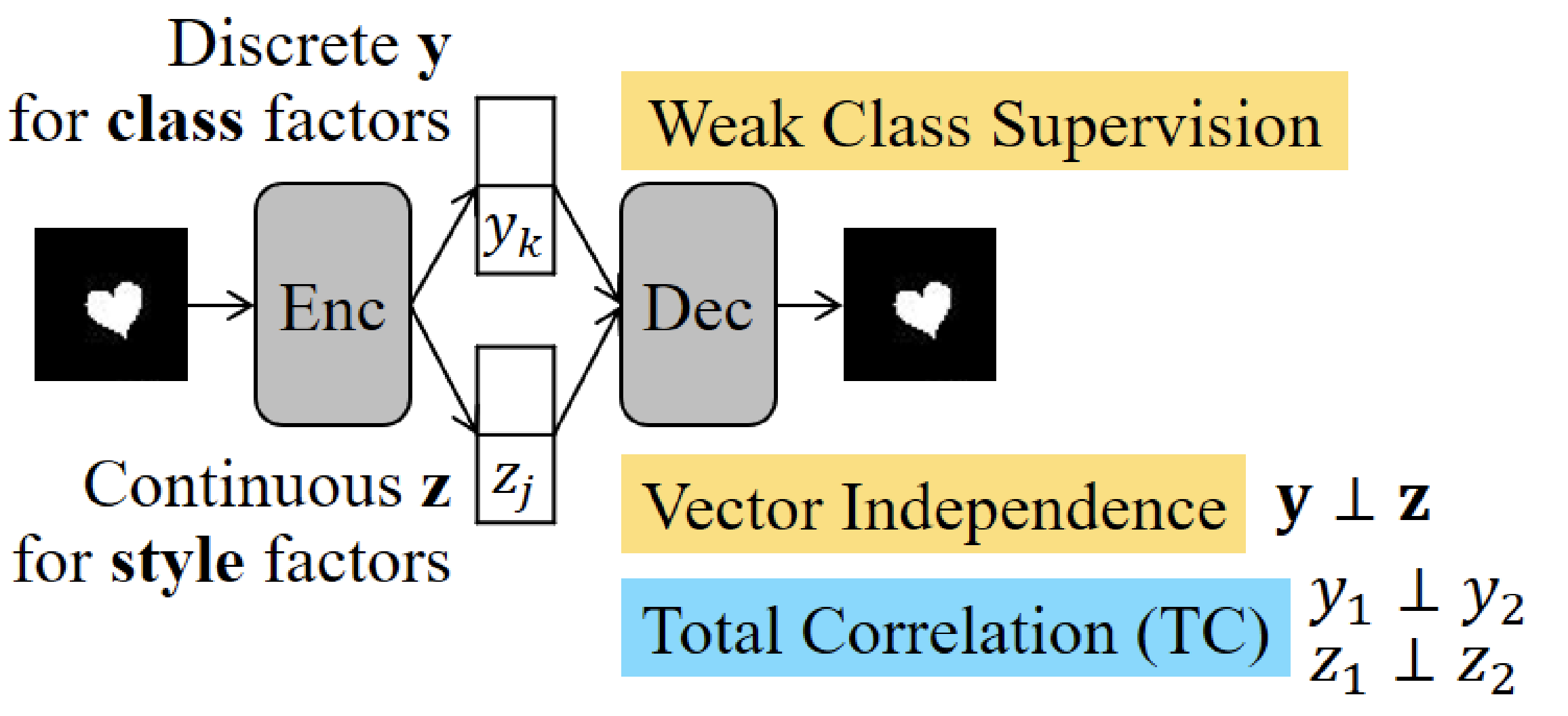
The goal is to obtain a nice latent representation $\mathbf z$ for our inputs $\mathbf x$. To do this, we learn parameters $\phi$ for the encoder $p_\phi( \mathbf z\vert \mathbf x)$ and $\theta$ for the decoder $q_{\mathbf \theta} ( \mathbf x\vert \mathbf z)$. We do this with the standard vae setup, whereby a code $z$ is sampled, using the output of the encoder (intro to VAEs here).

disentangled vae losses

reconstruction loss	compactness prior loss	total correlation loss
encourages accurate reconstruction of the input	encourages points to be compactly placed in space	encourages latent variables to be independent

summarizing the losses
- reconstruction loss - measures the quality of the reconstruction, the form of the loss changes based on the assumed distribution of the likelihood of each pixel
  - binary cross entropy loss - corresopnds to bernoulli distr., most common - doesn’t penalize (0.1, 0.2) and (0.4, 0.5) the same way, which might be problematic
  - mse loss - gaussian distr. - tends to focus on a fex pixels that are very wrong
  - l1 loss - laplace distr.
- compactness prior loss
  - doesn’t use the extra injected latent noise
  - tries to push all the points to the same place
  - emphasises smoothness of z, using as few dimensions of z as possible, and the main axes of z to capture most of the data variability
  - usually assume prior is standard normal, resulting in pushing the code means to 0 and code variance to 1
  - we can again split this term $\sum_i \corange{\underbrace{\text{KL} \left(p_\phi( \mathbf z_i\vert \mathbf x)\:\vert\vert\:prior(\mathbf z_i) \right)}_{\text{compactness prior loss}}} = \cpurple{\underbrace{\sum_i I(x; z)}_{\text{mutual info}}} + \cpink{\underbrace{\text{KL} \left(p_\phi( \mathbf z_i)\:\vert\vert\:prior(\mathbf z_i) \right)}_{\text{factorial prior loss}}}$
    - (see factor-vae paper for proof (kim & mnih 2018))
- total correlation loss - encourages factors to be independent
  - measures dependence between marginals of the latent vars
  - intractable (requires pass through the whole dset)
  - instead sample $dec_\phi(\mathbf z\vert \mathbf x)$ and create $\prod_j dec_\phi( \mathbf z_i\vert \mathbf x) $ by permuting across the batch dimension
    - now, calculate the kl with the density-ratio trick - train a classifier to approximate the ratio from these terms

disentangled vae in code

# Reconstruction + KL divergence losses summed over all elements and batch
def loss_function(x_reconstructed, x, mu, logvar, beta=1):
  '''
  Params
  ------
  x_reconstructed: torch.Tensor
		Reconstructed input, with values between 0-1
	x: torch.Tensor
		input, values unrestricted
  '''
  
  # reconstruction loss (assuming bernoulli distr.)
  # BCE = sum_i [x_rec_i * log(x_i) + (1 - x_rec_i) * log(1-x_i)]
	rec_loss = F.binary_cross_entropy(x_reconstructed, x, reduction='sum')

  # compactness prior loss
	# 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
	KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
  
  # total correlation loss (calculate tc-vae way)
	z_sample = mu + torch.randn_like(exp(0.5 * logvar))
	log_pz, log_qz, log_prod_qzi, log_q_zCx = func(z_sample, mu, logvar)
  # I[z;x] = KL[q(z,x)\vert\vertq(x)q(z)] = E_x[KL[q(z\vertx)\vert\vertq(z)]]
  mi_loss = (log_q_zCx - log_qz).mean()
  # TC[z] = KL[q(z)\vert\vert\prod_i z_i]
  tc_loss = (log_qz - log_prod_qzi).mean()
  # dw_kl_loss is KL[q(z)\vert\vertp(z)] instead of usual KL[q(z\vertx)\vert\vertp(z))]
  dw_kl_loss = (log_prod_qzi - log_pz).mean()
  
	return rec_loss + beta * KLD

vaes for interpretation

icam (bass et al. 2020) - learn disentangled repr using vae with adv loss to make repr class-relevant
- va-gan (baumgartner et al. 2018) - interpret features in GAN space

various vaes

vae (kingma & welling, 2013)
beta-vae (higgins et al. 2017) - add hyperparameter $\beta$ to weight the compactness prior term
beta-vae H (burgess et al. 2018) - add parameter $C$ to control the contribution of the compactness prior term
- \[\overbrace{\mathbb E_{p_\phi(\mathbf z\vert \mathbf x)}}^{\text{samples}} [ \cblue{\underbrace{-\log q_{\mathbf \theta} ( \mathbf x\vert \mathbf z)}_{\text{reconstruction loss}}} ] + \textcolor{teal}{\beta}\; \vert\sum_i \corange{\underbrace{\text{KL} \left(p_\phi( \mathbf z_i\vert \mathbf x)\:\vert\vert\:prior(\mathbf z_i) \right)}_{\text{compactness prior loss}}} -C\vert\]
- C is gradually increased from zero (allowing for a larger compactness prior loss) until good quality reconstruction is achieved
factor-vae (kim & minh 2018) - adds total correlation loss term
- computes total correlation loss term using discriminator (can we discriminate between the samples when we shuffle over the batch dimension or not?)
- beta-TC-VAE = beta-total-correlation VAE (chen et al. 2018) - same objective but computed without need for discriminator
  - use minibatch-weighted sampling to compute each of the 3 terms that make up the original VAE compactness prior loss
  - main idea is to better approximate $q(z)$ by weighting samples appropriately - biased, but easier to compute
- Interpretable VAEs for nonlinear group factor analysis (ainsworth et al. 2018)
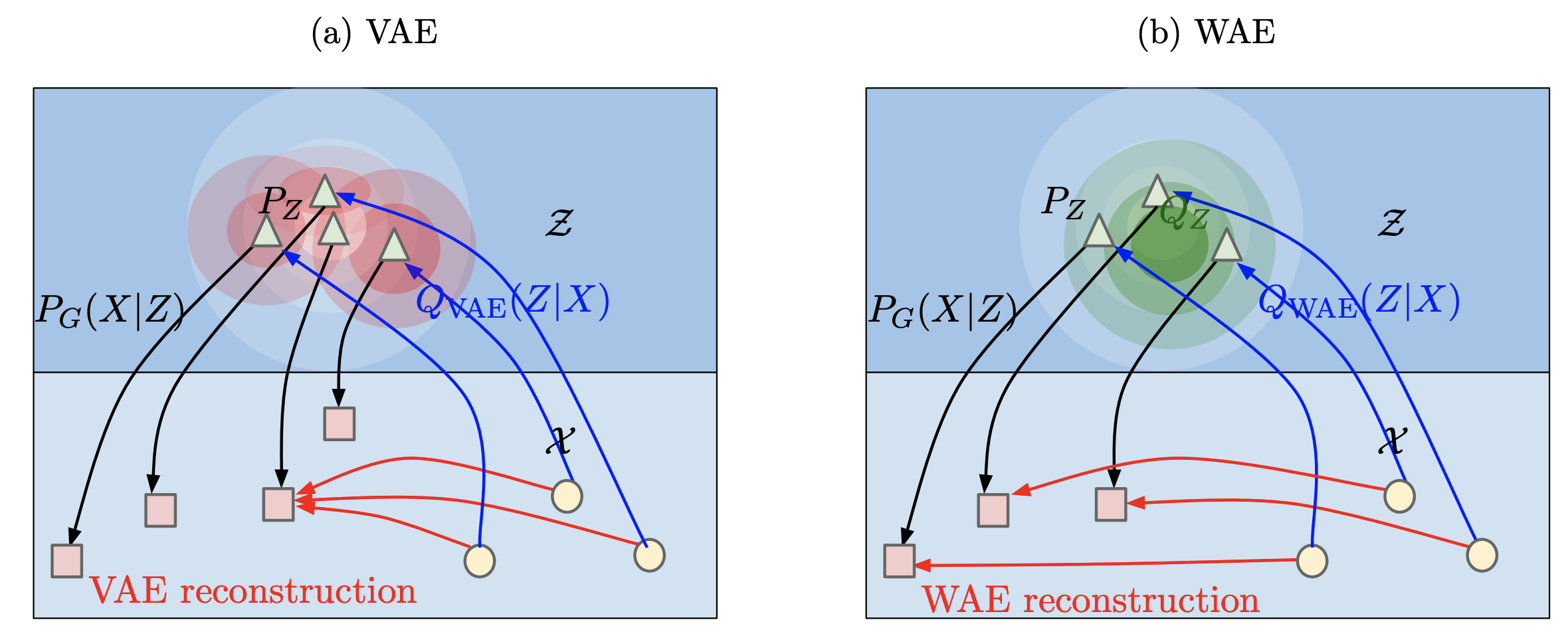
Wasserstein Auto-Encoders (tolstikhin et al.) - removes the mutual info part of the loss
- wasserstein distance = earth-movers distance, how far apart are 2 distrs
- minimizes wasserstein distance + penalty which is similar to auto-encoding penalty, without the mutual info term
- another intuition: rather than map each point to a ball (since VAE adds noise to each latent repr), we only constraint the overall distr of Z, potentially making reconstructions less blurry (but potentially making latent space less smooth)
Adversarial Latent Autoencoder (pidhorskyi et al. 2020)
- improve quality of generated VAE reconstructions by using a different setup which allows for using a GAN loss
Variational Autoencoders Pursue PCA Directions (by Accident) (rolinek et al. 2018)
- local orthogonality of the embedding transformation
- prior $p(z)$ is standard normal, so encoder is assumed to be Gaussian with a certain mean, and diagonal covariance
- disentanglement is sensitive to rotations of the latent embeddings but reconstruction err doesn’t care
- for linear autoencoder w/ square-error as reconstruction loss, we recover PCA decomp
Disentangling Disentanglement in Variational Autoencoders (2019)
- independence can be too simplistic, instead 2 things:
  - the latent encodings of data having an appropriate level of overlap
    - keeps encodings from just being a lookup table
    - when encoder is unimodal, $I(x; z)$ gives us a good handle on this
  - prior structure on the latents (e.g. independence, sparsity)
- to trade these off, can penalize divergence between $q_\phi(z)$ and $p(z)$
- nonisotropic priors - isotropic priors are only good up to rotation in the latent space
  - by chossing a nonisotropic prior (e.g. nonisotropic gaussian), can learn certain directions more easily
- sparse prior - can help do clustering
VAE-SNE: a deep generative model for simultaneous dimensionality reduction and clustering (graving & couzin 2020) - reduce dims + cluster without specifying number of clusters
- objective
  \[\begin{aligned} \underset{\boldsymbol\theta,\boldsymbol\phi}{\arg\min}\; -\text{SNELBO}(\mathbf X,\boldsymbol\theta,\boldsymbol\phi) &= \underset{\boldsymbol\theta,\boldsymbol\phi}{\arg\min}\; -\frac{1}{N}\sum_i \text{ELBO}_i(\mathbf x_i,\boldsymbol\theta,\boldsymbol\phi) - \alpha\, \text{SNE}_i(\mathbf X,\boldsymbol\phi) \\ \text{ELBO}_i(\mathbf x_i,\boldsymbol\theta,\boldsymbol\phi) &= \gamma\, \mathbb E_{\mathbf z_i\sim q_{\boldsymbol\phi}(\mathbf z \vert \mathbf x_i)} \underbrace{\left[\log p_{\boldsymbol\theta}(\mathbf x_i \vert \mathbf z_i)\right]}_{\text{distortion}} - \beta\, \underbrace{\mathbb{KL}\left[q_{\boldsymbol\phi}(\mathbf z \vert \mathbf x_i) \,\Vert\, p_{\boldsymbol\theta}(\mathbf z)\right]}_{\text{rate}} \\ \text{SNE}_i(\mathbf X,\boldsymbol\phi) &= \mathbb E_{\substack{\mathbf z_i\sim q_{\boldsymbol\phi}(\mathbf z \vert \mathbf x_i) \\ \mathbf z_j\sim q_{\boldsymbol\phi}(\mathbf z \vert \mathbf x_j)}} \left[\sum_j \text{SNE}_{j \vert i}(\mathbf x_i,\mathbf x_j,\boldsymbol\phi)\right] \\ &= \mathbb E_{\substack{\mathbf z_i\sim q_{\boldsymbol\phi}(\mathbf z \vert \mathbf x_i) \\ \mathbf z_j\sim q_{\boldsymbol\phi}(\mathbf z \vert \mathbf x_j)}} \underbrace{\left[\sum_j \mathbb{KL}\Big[\overbrace{p(\mathbf x_j \vert \mathbf x_i)}^{\text{dist in original space}} \,\Big\Vert\, \underbrace{q_{\boldsymbol\phi}(\mathbf z_j \vert \mathbf z_i)}_{\text{dist in latent space}}\Big]\right]}_{\text{pairwise similarity}} \end{aligned}\]
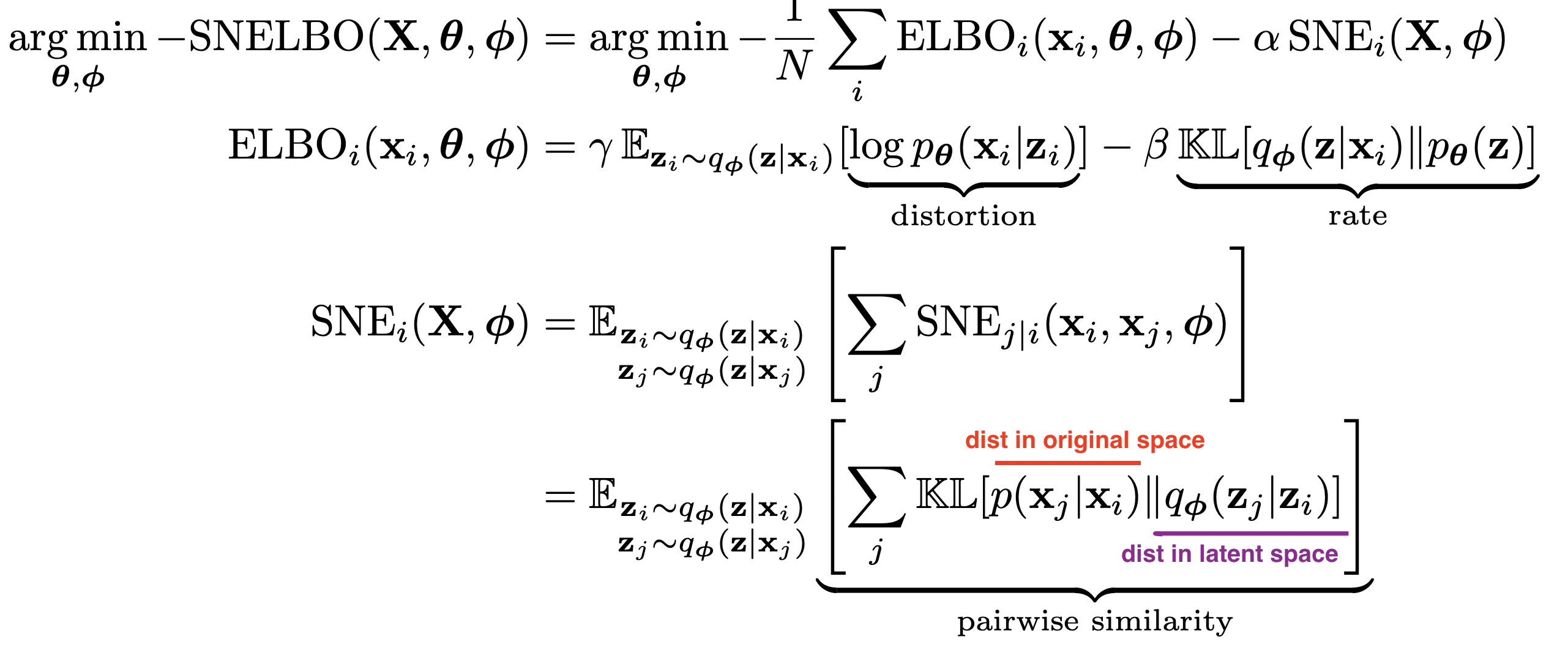
- stochastic neighbor regularizer that optimizes pairwise similarity kernels between original and latent distrs. to strengthen local neighborhood preservation
  - can use different neighbor kernels, e.g. t-SNE similarity (van der Maaten & Hinton, 2008) or Gaussian SNE kernel (Hinton & Roweis, 2003)
  - perplexity annealing technique (Kobak and Berens, 2019) - decay the size of local neighborhoods during training (helps to preserve structure at multiple scales)
- Gaussian mixture prior for learning latent distr. (with very large number of clusters)
  - at the end, merge clusters using a sparse watershed (see todd et al. 2017)
- extensive evaluation - test several datasets / methods and evaluate how well the first 2 dimensions preserve the following:
  - global - correlation between pairwise distances in orig/latent spaces
  - local - both metric (distance- or radius-based) and topological (neighbor-based) neighborhoods which are 1% of total embedding size
  - fine-scale - neighborhoods which are <1% of total embedding size
  - temporal info (for time-series data only) - correlation between latent and original temporal derivatives
  - likelihood on out-of-sample data
- further advancements
  - embed into polar coordinates (rather than Euclidean) helps a lot
  - convolutional VAE-SNE - extract features from images using some pre-trained net and then run VAE-SNE on these features
- background: earlier works also used SNE objective for regularization - starts with van der Maaten 2009 (parametric t-SNE)
- future work: density-preserving versions of t-SNE, modeling hierarchical structure in vae, conditional t-SNE kernel
A Survey of Inductive Biases for Factorial Representation-Learning (ridgeway 2016)
- desiderata
  - compact
  - faithful - preserve info required for task
  - explicitly represent the attributes required for the task at hand
  - interpretable by humans
- factorial representation - attributes are statistically independent and can provide a userful bias for learning
  - “compete” - factors are more orthogonal
  - “cooperate” - factors are more similar
  - bias on distribution of factors
    - PCA - minimize reconstruction err. subject to orthogonal weights
    - ICA - maximize non-Gaussianity (can also have sparse ICA)
  - bias on factors being invariant to certain types of changes
    - ISA (independent subspace analysis) - 2 layer model where first layer is linear, 2nd layer pools first layer (not maxpool, more like avgpool), sparsity at second layer
      - i.e. 1st layer cooperates, 2nd layer competes
    - VQ - vector quantizer - like ISA but first layer filters now compete and 2nd layer cooperates
    - SOM - encourages topographic map by enforcing nearby filters to be similar
  - bias in how factors are combined
    - linear combination - PCA/ICA
    - multilinear models - multiplicative interactions between factors (e.g on top of ISA)
    - functional parts - factor components are combined to construct the output
      - ex. NMF - parts can only add, not substract to total output
      - ex. have each pixel in the output be represented by only one factor in a VQ
    - hierarchical layers
      - ex. R-ICA - recursive ICA - run ICA on coefficients from previous layer (after some transformation)
- supervision bias
  - constraints on some examples
    - e.g. some groups have same value for a factor
    - e.g. some examples have similar distances (basis for MDS = multidimensional scaling)
    - e.g. analogies between examples
    - can do all of these things with auto-encoders
more papers
- infoVAE
- dipVAE
- vq-vae - latent var is discrete, prior is learned
- Learning Disentangled Representations with Semi-Supervised Deep Generative Models
  - specify graph structure for some of the vars and learn the rest

GANs

model-based (disentangle during training)

disentangling architectures
- InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets (chen et al. 2016)
  - encourages $I(x; c)$ to be high for a subset of the latent variables $z$
    - slightly different than vae - defined under the distribution $p(c) p(x\vert c)$ whereas vae uses $p_{data}(x)enc(z\vert x)$
  - mutual info is intractable so optimizes a lower bound
- Stylegan (karras et al. 2018)
  - introduced perceptual path length and linear separability to measure the disentanglement property of latent space
  - Stylegan2 (karras et al. 2019):
    - $\psi$ scales the deviation of w from the average - $\psi=1$ is original, moving towards 0 improves quality but reduces variety
    - also has jacobian penalty on mapping from style space $w$ to output image $y$
DNA-GAN: Learning Disentangled Representations from Multi-Attribute Images (xiao et al. 2017)
Clustering by Directly Disentangling Latent Space (ding et al. 2019) - clustering in the latent space of a gan
Semi-Supervised StyleGAN for Disentanglement Learning (nie et al. 2020) - further improvements on StyleGAN using labels in the training data
The Hessian Penalty: A Weak Prior for Unsupervised Disentanglement (peebles et al. 2020)
- if we perturb a single component of a network’s input, then we would like the change in the output to be independent of the other input components
- minimize off-diagonal entries of Hessian matrix (can be obtained with finite differences)
  - smoother + more disentangled + shrinkage in latent space
- Hessian penalty is for a scalar - they define penalty as max penalty over Hessian over all pixels in the generator
- unbiased stochastic estimator for the Hessian penalty (Hutchinson estimator)
- they apply this penalty with $z$ as input, but different intermediate activations as output

post-hoc (disentangle after training)

mapping latent space
- InterFaceGAN: Interpreting the Disentangled Face Representation Learned by GANs (shen et al. 2020)
- Interpreting the Latent Space of GANs for Semantic Face Editing (shen et al. 2020)
  - find latent directions for each binary attribute, as directions which separate the classes using linear svm
    - validation accuracies in tab 1 are high…much higher for all data (because they have high confidence level on attribute scores maybe) - for PGGAN but not StyleGAN
  - intro of this paper gives good survey of how people have studied GAN latent space
  - few papers posthoc analyze learned latent repr.
- On the “steerability” of generative adversarial networks (jahanian et al. 2020)
  - learn to approximate edits to images, such as zooms
    - linear walk is as effective as more complex non-linear walks for learning this
    - nonlinear setting - learn a neural network which applies a small perturbation in a specific direction (e.g. zooming)
      - to move further in this space, repeatedly apply the function
- A Disentangling Invertible Interpretation Network for Explaining Latent Representations (esser et al. 2020) - map latent space to interpretable space, with invertible neural network
  - interpretable space factorizes, so is disentangled
  - individual concepts (e.g. color) can use multiple interpretable latent dims
  - instead of user-supplied interpretable concepts, user supplies two sketches which demonstrate a change in a concept - these sketches are used w/ style transfer to create data points which describe the concept
  - alternatively, with no user-supplied concepts, try to get independent components in unsupervised way
- Disentangling in Latent Space by Harnessing a Pretrained Generator (nitzan et al. 2020)
  - learn to map attributes onto latent space of stylegan
  - works using two images at a time and 2 encoders
    - for each image, predict attributes + identity, then mix the attributes
  - results look realy good, but can’t vary one attribute at a time (have to transfer all attributes from the new image)
- ELEGANT: Exchanging Latent Encodings with GAN for Transferring Multiple Face Attributes (xiao et al. 2018)
  - trains 2 images at a time - swap an attribute that differs between the images and reconstruct images that have the transferred attribute
bias
- Towards causal benchmarking of bias in computer vision algorithms (balakrishnan et al. 2020) - use human annotations to disentangle latent space
  - synthesis approach can alter multiple attributes at a time to produce grid-like matched samples of images we call transects
  - find directions + orthogonalize same as shen et al. 2020
- Detecting Bias with Generative Counterfactual Face Attribute Augmentation (denton et al. 2019) - identify latent dims by training a classifier in the latent space on groundtruth attributes of the training images
- Explaining Classifiers with Causal Concept Effect (CaCE) (goyal et al. 2020) - use vae to disentangle / alter concepts to probe classifier
post-hoc
- Explanation by Progressive Exaggeration (singla et al. 2019)
  - progressively change image to negate the prediction, keeping most features fixed
    - want to learn mapping $I(x, \delta)$ which produces realistic image that changes features by $\delta$
  - 3 losses: data consistency (perturbed samples should look real), prediction changes (perturbed samples should appropriately alter prediction), self-consistency (applying reverse perturbatino should bring x back to original, and $\delta=0$ should return identity)
  - moving finds ways to generate images that do change the wanted attribute (and don’t change the others too much)
  - minor
    - used human experiments
    - limited to binary classification
- Interpreting Deep Visual Representations via Network Dissection (zhou et al. 2017)
  - obtain image attributes for each z (using classifier, not human labels)
    - this classifier may put bias back in
  - to find directions representing an attribute, train a linear model to predict it from z
- GAN Dissection: Visualizing and Understanding Generative Adversarial Networks (bau et al. 2018) - identify group of interpretable units based on segmentation of training images
  - find directions which allow for altering the attributes
- GANSpace: Discovering Interpretable GAN Controls (härkönen et al. 2020) - use PCA in the latent space (w for styleGAN, activation-space at a specific layer for BigGAN) to select directions
- Editing in Style: Uncovering the Local Semantics of GANs (collins et al. 2020) - use k-means on gan activations to find meaningful clusters (with quick human annotation)
  - add style transfer using target/source image
- Unsupervised Discovery of Interpretable Directions in the GAN Latent Space (voynov & babenko 2020) - loss function which tries to recover random shifts made to the latent space

misc

Learning Diverse and Discriminative Representations via the Principle of Maximal Coding Rate Reduction (yu, …, & ma, 2020)
- goal: learn low-dimensional structure from high-dim (labeled or unlabeled) data
- approach: instead of cross-entropy loss, use maximal coding rate reduction = MCR loss function to learn linear feature space where:
  - inter-class discriminative - features of samples from different classes/clusters are uncorrelated + different low-dim linear subspaces
  - intra-class compressible - features of samples from same class/cluster are correlated (i.e. belong to low-dim linear subspace)
  - maximally diverse - dimension (or variance) of features for each class/cluster should be as large as possible as long as uncorrelated from other classes/clusters
- related to nonlinear generalized PCA
- given random variable $z$ and precision $\epsilon$, rate distortion $R(z, \epsilon)$ is minimal number of bits to encode $z$ such that expected decoding err is less than $\epsilon$
  - can compute from finite samples
  - can compute for each class (diagonal matrices represent class/cluster membership in loss function)
  - MCR maximizes (rate distortion for all features) - (rate distortion for all data separated into classes)
    - like a generalization of information gain
- evaluation
  - with label corruption performs better
Learned Equivariant Rendering without Transformation Supervision (resnick et al. 2020) - separate foreground / background using video

(semi)-supervised disentanglement

these papers use some form of supervision for the latent space when disentangling

Semi-supervised Disentanglement with Independent Vector Variational Autoencoders (kim et al. 2020)
Learning Disentangled Representations with Semi-Supervised Deep Generative Models (siddharth et al. 2017) - put priors on interpretable variables during training and learn the rest
Weakly Supervised Disentanglement with Guarantees (shu et al. 2019)
- prove results on disentanglement for rank pairing
- different types of available supervision
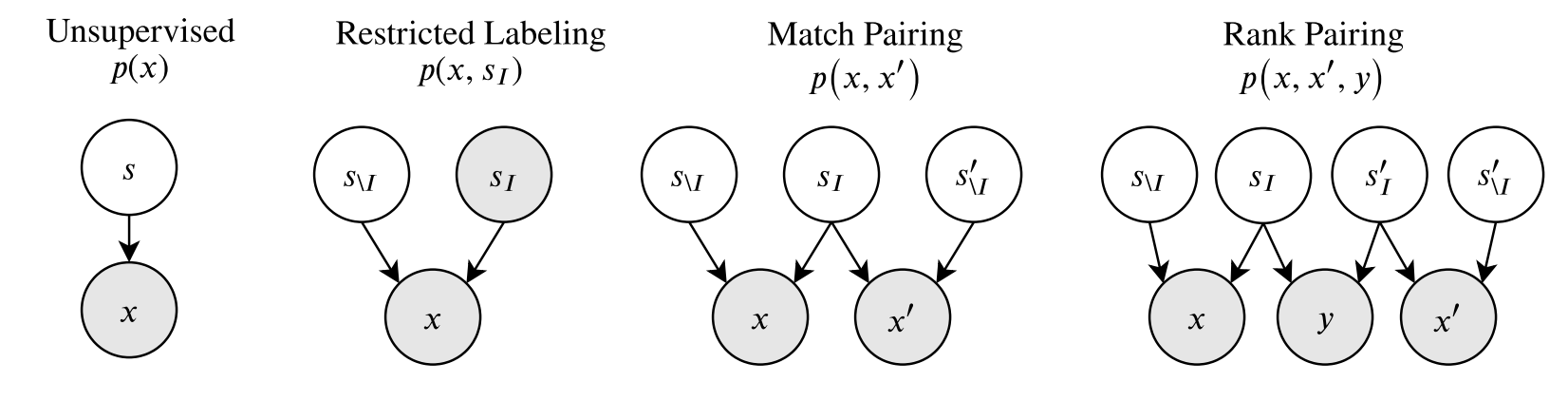
  - restricted labeling - given labels for some groundtruth factors (e.g. label “glasses”, “gender” for all images)
  - match pairing - given pairs or groups (e.g. these images all have glasses)
  - rank pairing - label whether a feature is greater than another (e.g. this image has darker skin tone than this one)
Weakly Supervised Disentanglement by Pairwise Similarities (chen & batmanghelich 2019) - use pairwise supervision

evaluating disentanglement

Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations (locatello et al. 2019)
- state of disentanglement is very poor…depends a lot on architecture/hyperparameters
- good way to evaluate: make explicit inductive biases, investigate benefits of this disentanglement
- defining disentanglement - compact, interpretable, independent, helpful for downstream tasks, causal inference
  - a change in one factor of variation should lead to a change in a single factor in the learned repr.
- unsupervised learning of disentangled reprs. is impossible without inductive biases
note - vae’s come with reconstruction loss + compactness prior loss which can be looked at on their own
data
- dsprites dataset has known latent factors we try to recover
beta-vae disentanglement metric score = higgins metric - see if we can capture known disentangled repr. using pairs of things where only one thing changes
- start with a known generative model that has an observed set of independent and interpretable factors (e.g. scale, color, etc.) that can be used to simulate data.
- create a dataset comprised of pairs of generated data for which a single factor is held constant (e.g. a pair of images which have objects with the same color).
- use the inference network to map each pair of images to a pair of latent variables.
- train a linear classifier to predict which interpretable factor was held constant based on the latent representations. The accuracy of this predictor is the disentanglement metric score.
Evaluating Disentangled Representations (sepliarskaia et al. 2019)
- defn 1 (Higgins et al., 2017; Kim and Mnih, 2018; Eastwood and Williams, 2018) = factorVAE metric: A disentangled representation is a representation where a change in one latent dimension corresponds to a change in one generative factor while being relatively invariant to changes in other generative factors.
- defn 2 (Locatello et al., 2018; Kumar et al., 2017): A disentangled representation is a representation where a change in a single generative factor leads to a change in a single factor in the learned representation.
- metrics
  - DCI: Eastwood and Williams (2018) - informativeness based on predicting gt factors using latent factors
  - SAP: Kumar et al. (2017) - how much does top latent factor match gt more than 2nd latent factor
  - mutual info gap MIG: Chen et al. 2018 - mutual info to compute the same thing
  - modularity (ridgeway & mozer, 2018) - if each dimension of r(x) depends on at most a factor of variation using their mutual info

non-deep methods

unifying vae and nonlinear ica (khemakhem et al. 2020)
- ICA
  - maximize non-gaussianity of $z$ - use kurtosis, negentropy
  - minimize mutual info between components of $z$ - use KL, max entropyd