---

uncertainty view markdown

Some notes on uncertainty in machine learning, particularly deep learning.

---

basics

• calibration - predicted probabilities should match real probabilities
  • platt scaling - given trained classifier and new calibration dataset, basically just fit a logistic regression from the classifier predictions -> labels
  • isotonic regression - nonparametric, requires more data than platt scaling
    • piecewise-constant non-decreasing function instead of logistic regression
• confidence - predicted probability = confidence, max margin, entropy of predicted probabilities across classes
• ensemble uncertainty - ensemble predictions yield uncertainty (e.g. variance within ensemble)
• quantile regression - use quantile loss to penalize models differently + get confidence intervals
  • can easily do this with sklearn
  • quantile loss = $\begin{cases} \alpha \cdot \Delta & \text{if} \quad \Delta > 0\\(\alpha - 1) \cdot \Delta & \text{if} \quad \Delta < 0\end{cases}$
    • $\Delta =$ actual - predicted
    • 
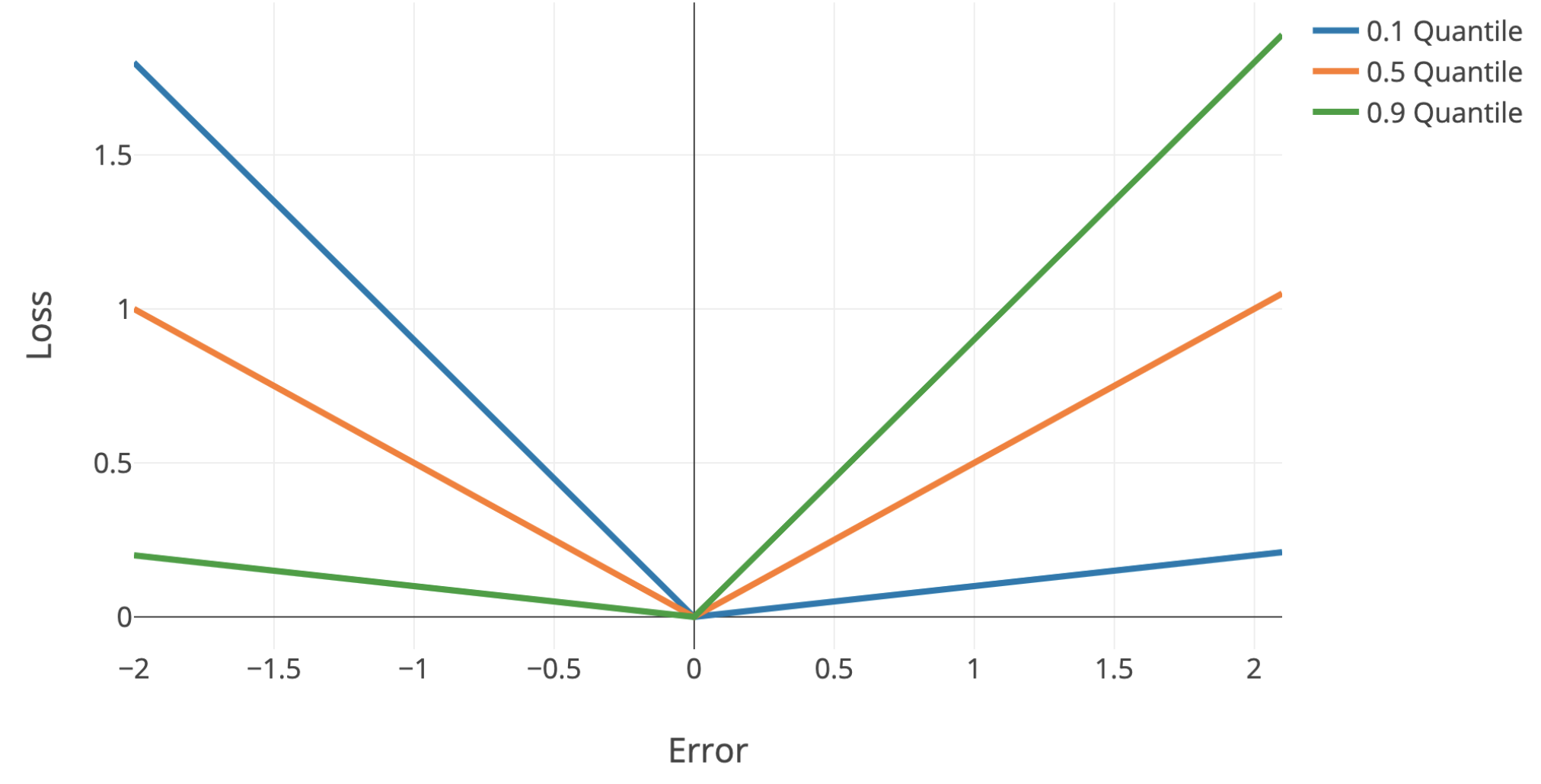
  • Single-Model Uncertainties for Deep Learning (tagovska & lopez-paz 2019) - use simultaneous quantile regression

outlier-detection

Note: outlier detection uses information only about X to find points “far away” from the main distribution

• overview from sklearn
  • elliptic envelope - assume data is Gaussian and fit elliptic envelop (maybe robustly) to tell when data is an outlier
  • local outlier factor (breunig et al. 2000) - score based on nearest neighbor density
  • idea: gradients should be larger if you are on the image manifold
  • isolation forest (liu et al. 2008) - lower average number of random splits required to isolate a sample means more outlier
  • one-class svm - estimates the support of a high-dimensional distribution using a kernel (2 approaches:)
    • separate the data from the origin (with max margin between origin and points) (scholkopf et al. 2000)
    • find a sphere boundary around a dataset with the volume of the sphere minimized (tax & duin 2004)
• detachment index (kuenzel 2019) - based on random forest
  • for covariate $j$, detachment index $d^j(x) = \sum_i^n w (x, X_i) \vert X_i^j - x^j \vert$
    • $w(x, X_i) = \underbrace{1 / T\sum_{t=1}^{T}}{\text{average over T trees}} \frac{\overbrace{1{ X_i \in L_t(x) }}^{\text{is } X_i \text{ in the same leaf?}}}{\underbrace{\vert L_t(x) \vert}{\text{num points in leaf}}}$ is $X_i$ relevant to the point $x$?

uncertainty detection

Note: uncertainty detection uses information about X / $\phi(X)$ and Y, to find points for which a particular prediction may be uncertain. This is similar to the predicted probability output by many popular classifiers, such as logistic regression.

• rejection learning - allow models to reject (not make a prediction) when they are not confidently accurate (chow 1957, cortes et al. 2016)
• To Trust Or Not To Trust A Classifier (jiang, kim et al 2018) - find a trusted region of points based on nearest neighbor density (in some embedding space)
  • trust score uses density over some set of nearest neighbors
  • do clustering for each class - trust score = distance to once class’s cluster vs the other classes
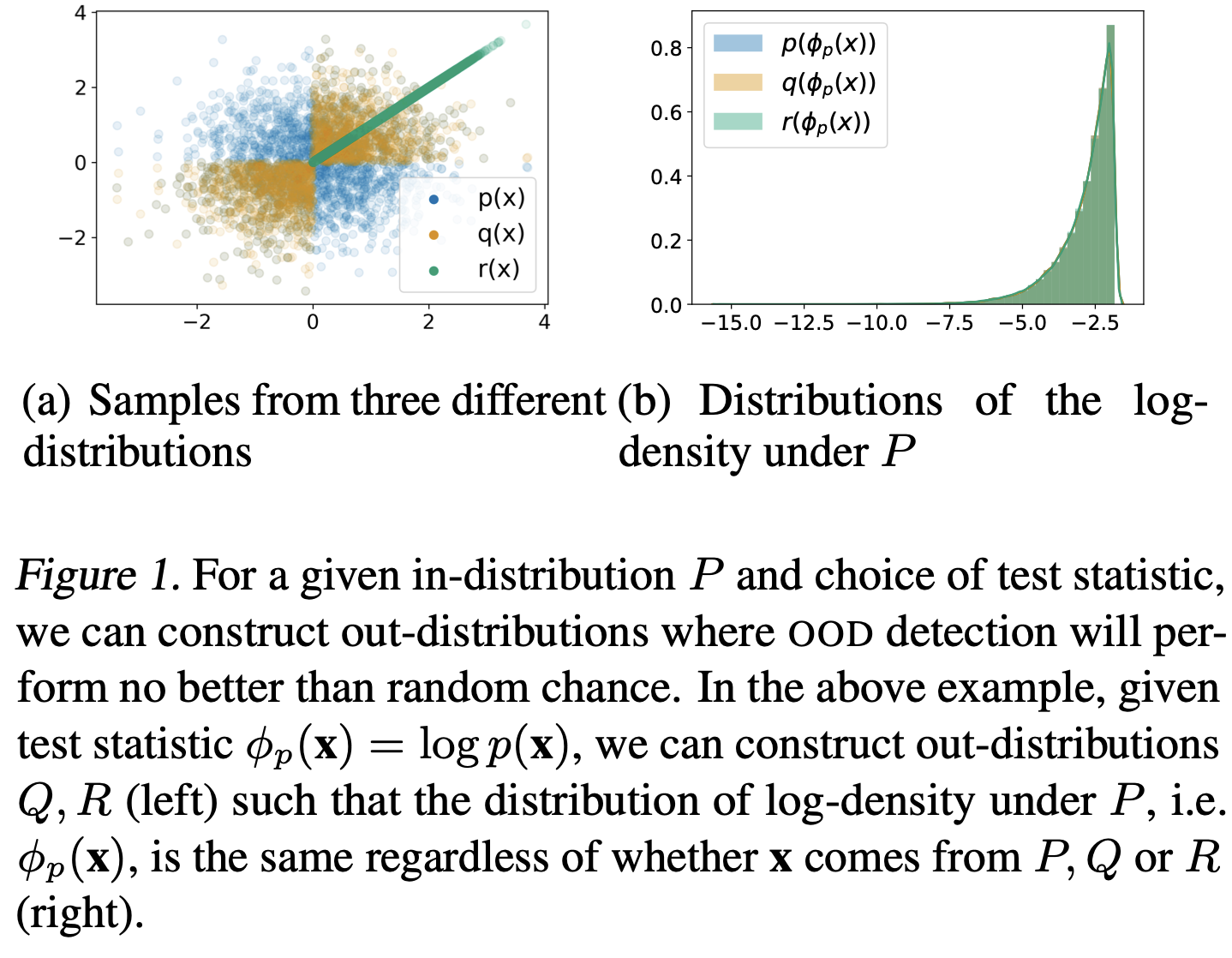
• Understanding Failures in Out-of-Distribution Detection with Deep Generative Models (zhang…ranganath, 2021) - explicit likelihood DGMs (e.g. autoregressive models, normalizing flows) have been shown to assign higher likelihoods to unrelated inputs than even those from the training distribution
  • OOD detection has been defined as the task of identify- ing “whether a test example is from a different distr. from the training data” (Hendrycks & Gimpel, 2017)
  • without any constraints on out-distributions, the task of OOD detection is impossible
  • 

bayesian approaches

• epistemic uncertainty - uncertainty in the DNN model parameters
  • without good estimates of this, often get aleatoric uncertainty wrong (since $p(y\vert x) = \int p(y \vert x, \theta) p(\theta \vert data) d\theta$
• aleatoric uncertainty - inherent and irreducible data noise (e.g. features contradict each other)
  • this can usually be gotten by predicting a distr. $p(y \vert x)$ instead of a point estimate
  • ex. logistic reg. already does this
  • ex. regression - just predict mean and variance of Gaussian
• gaussian processes

neural networks

ensembles

• DNN ensemble uncertainty works - predict mean and variance w/ each network then ensemble (don’t need to do bagging, random init is enough)
• Deep Ensembles: A Loss Landscape Perspective (fort, hu, & lakshminarayanan, 2020)
  • different random initializations provide most diversity
  • samples along one path have varying weights but similar predictions
  • 
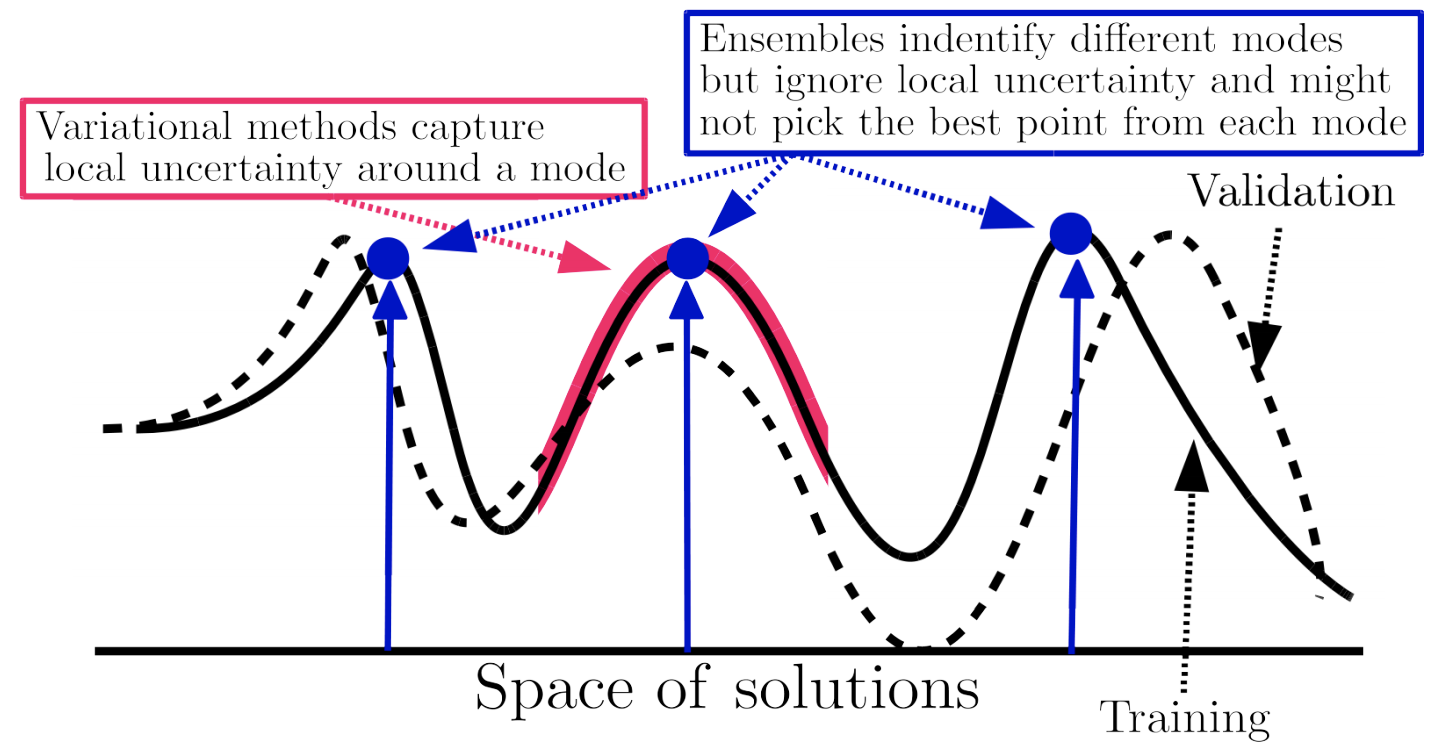
• Pitfalls of In-Domain Uncertainty Estimation and Ensembling in Deep Learning - many complex ensemble approaches are similar to just an ensemble of a few randomly initialized DNNs

directly predict uncertainty

• Inhibited Softmax for Uncertainty Estimation in Neural Networks (mozejko et al. 2019) - directly predict uncertainty by adding an extra output during training
• Learning Confidence for Out-of-Distribution Detection in Neural Networks (devries et al. 2018) - predict both prediction p and confidence c
  • during training, learn using $p’ = c \cdot p + (1 - c) \cdot y$
• Bias-Reduced Uncertainty Estimation for Deep Neural Classifiers (geifmen et al. 2019)
  • just predicting uncertainty is biased
  • estimate uncertainty of highly confident points using earlier snapshots of the trained model
• Contextual Outlier Interpretation (liu et al. 2018) - describe outliers with 3 things: outlierness score, attributes that contribute to the abnormality, and contextual description of its neighborhoods
  • Energy-based Out-of-distribution Detection (liu et al. 2021)
• Getting a CLUE: A Method for Explaining Uncertainty Estimates
• The Right Tool for the Job: Matching Model and Instance Complexities - ACL Anthology - at each layer, model outputs a prediction - if it’s confident enough it returns, otherwise it continues on to the next layer

nearest-neighbor methods

• Deep k-Nearest Neighbors: Towards Confident, Interpretable and Robust Deep Learning (papernot & mcdaniel, 2018)
• distance-based confidence scores (mandelbaum et al. 2017) - use either distance in embedding space or adversarial training to get uncertainties for DNNs
• deep kernel knn (card et al. 2019) - predict labels based on weighted sum of training instances, where weights are given by distance in embedding space
  • add an uncertainty based on conformal methods

bayesian neural networks

• blog posts on basics

  • want $p(\theta

    x) = \frac {p(x

    \theta) p(\theta)}{p(x)}$

    • $p(x)$ is hard to compute
• slides on basics
• Bayes by backprop (blundell et al. 2015) - efficient way to train BNNs using backprop
  • Instead of training a single network, trains an ensemble of networks, where each network has its weights drawn from a shared, learned probability distribution. Unlike other ensemble methods, the method typically only doubles the number of parameters yet trains an infinite ensemble using unbiased Monte Carlo estimates of the gradients.
• Evaluating Scalable Bayesian Deep Learning Methods for Robust Computer Vision
• icu bayesian dnns
  • focuses on epistemic uncertainty
  • could use one model to get uncertainty and other model to predict
• Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning
  • dropout at test time gives you uncertainty
• SWAG (maddox et al. 2019) - start with pre-trained net then get Gaussian distr. over weights by training with large constant setp-size
• Efficient and Scalable Bayesian Neural Nets with Rank-1 Factors (dusenberry, jerfel et al. 2020) - BNNs scale to SGD-level with better calibration

conformal inference

• conformal inference constructs valid (wrt coverage error) prediction bands for individual forecasts
  • relies on few parametric assumptions
  • holds in finite samples for any distribution of (X, Y) and any algorithm $\hat f$
  • starts with vovk et al. ‘90
• simple example: construct a 95% interval for a new sample (not mean) by just looking at percentiles of the empirical data
  • empirical data tends to undercover (since empirical residuals tend to underestimate variance) - conformal inference aims to rectify this
• Uncertainty Sets for Image Classifiers using Conformal Prediction (angelopoulos, bates, malik, jordan, 2021)
  • Image-to-Image Regression with Distribution-Free Uncertainty Quantification and Applications in Imaging (Angelopoulos, …jordan, malik, upadhyayula, roman, ‘22)
    • pixel-level uncertainties

---