Deep Learning view markdown

This note covers miscellaneous deep learning, with an emphasis on different architectures + empirical tricks.

See also notes in 📌 unsupervised learning, 📌 disentanglement, 📌 nlp, 📌 transformers

historical top-performing nets

  • LeNet (1998)
    • first, used on MNIST
  • AlexNet (2012)
    • landmark (5 conv layers, some pooling/dropout)
  • ZFNet (2013)
    • fine tuning and deconvnet
  • VGGNet (2014)
    • 19 layers, all 3x3 conv layers and 2x2 maxpooling
  • GoogLeNet (2015)
    • lots of parallel elements (called Inception module)
  • Msft ResNet (2015)
    • very deep - 152 layers
      • connections straight from initial layers to end
      • only learn “residual” from top to bottom
  • Region Based CNNs (R-CNN - 2013, Fast R-CNN - 2015, Faster R-CNN - 2015)
    • object detection
  • Generating image descriptions (Karpathy , 2014)
    • RNN+CNN
  • Spatial transformer networks (2015)
    • transformations within the network
  • Segnet (2015)
    • encoder-decoder network
  • Unet (Ronneberger, 2015)
    • applies to biomedical segmentation
  • Pixelnet (2017) - predicts pixel-level for different tasks with the same architecture - convolutional layers then 3 FC layers which use outputs from all convolutional layers together
  • Squeezenet
  • Yolonet
  • Wavenet
  • Densenet
  • NASNET
  • Efficientnet (2019)

basics

  • basic perceptron update rule
    • if output is 0, label is 1: increase active weights
    • if output is 1, label is 0: decrease active weights
  • perceptron convergence thm - if data is linearly separable, perceptron learning algorithm wiil converge
  • transfer / activation functions
    • sigmoid(z) = $\frac{1}{1+e^{-x}} = \frac{e^x}{e^x+1}$
    • Binary step
    • TanH (preferred to sigmoid)
    • Rectifier = ReLU
      • Leaky ReLU - still has some negative slope when <0
      • rectifying in electronics converts analog -> digital
    • rare to mix and match neuron types
  • deep - more than 1 hidden layer
  • mean-squared error (regression loss) = $\frac{1}{2}(y-\hat{y})^2$
  • cross-entropy loss (classification loss) = $=-\sum_j y_j \ln \hat{p}_j$
    • for binary classification, $y_j$ would take on 0 or 1 and $\hat y_j$ would be a probability
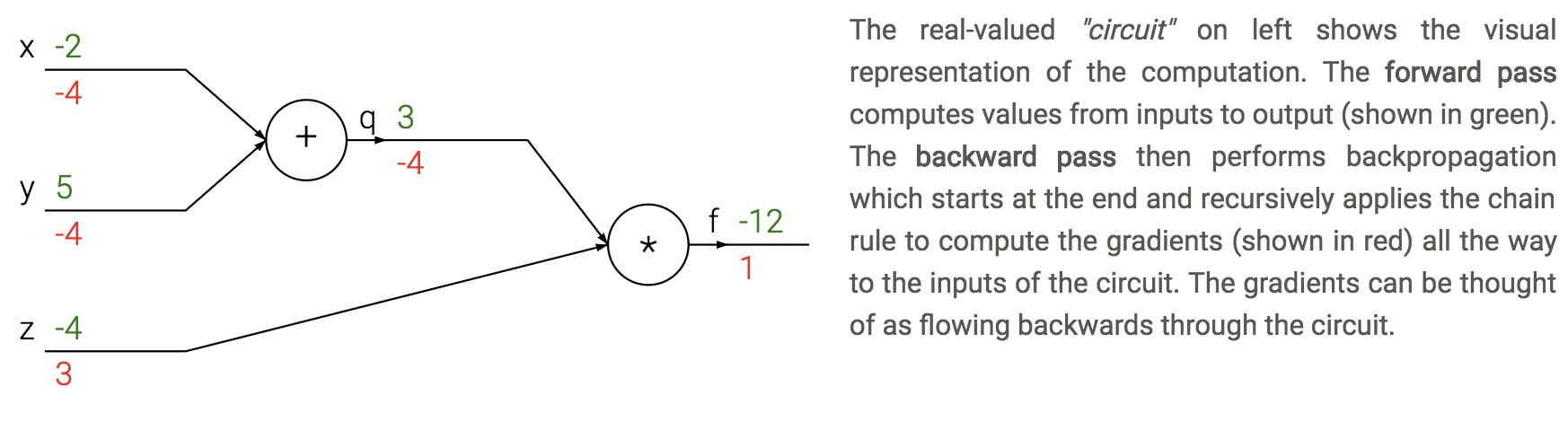
  • backpropagation - application of reverse mode automatic differentiation to neural networks’s loss
    • apply the chain rule from the end of the program back towards the beginning
      • $\frac{dL}{d \theta_i} = \frac{dL}{dz} \frac{\partial z}{\partial \theta_i}$
      • sum $\frac{dL}{dz}$ if neuron has multiple outputs z
      • L is output
    • $\frac{\partial z}{\partial \theta_i}$ is actually a Jacobian (deriv each $z_i$ wrt each $\theta_i$ - these are vectors)
      • each gate usually has some sparsity structure so you don’t compute whole Jacobian
  • pipeline
    • initialize weights, and final derivative ($\frac{dL}{dL}=1$)
    • for each batch
      • run network forward to compute outputs at each step
      • compute gradients at each gate with backprop
      • update weights with SGD
  • backprop

training

  • vanishing gradients problem - neurons in earlier layers learn more slowly than in later layers
    • happens with sigmoids
    • dead ReLus
  • exploding gradients problem - gradients are significantly larger in earlier layers than later layers
    • RNNs
  • batch normalization - whiten inputs to all neurons (zero mean, variance of 1)
    • do this for each input to the next layer
  • dropout - randomly zero outputs of p fraction of the neurons during training
    • like learning large ensemble of models that share weights
    • 2 ways to compensate (pick one)
      1. at test time multiply all neurons’ outputs by p
      2. during training divide all neurons’ outputs by p
  • softmax - takes vector z and returns vector of the same length
    • makes it so output sums to 1 (like probabilities of classes)
  • tricks to squeeze out performance
    • ensemble models
    • (stochastic) weight averaging can help a lot
    • test-time augmentation
      • this could just be averaging over dropout resamples as well
    • gradient checkpointing (2016 paper)
      • 10x larger DNNs into memory with 20% increase in comp. time
      • save gradients for a carefully chosen layer to let you easily recompute

CNNs

  • kernel here means filter
  • convolution G- takes a windowed average of an image F with a filter H where the filter is flipped horizontally and vertically before being applied
  • G = H $\ast$ F
    • if we do a filter with just a 1 in the middle, we get the exact same image
    • you can basically always pad with zeros as long as you keep 1 in middle
    • can use these to detect edges with small convolutions
    • can do Guassian filters
  • 1st-layer convolution typically sum over all color channels
  • 1x1 conv - still convolves over channels
  • pooling - usually max - doesn’t pool over depth
    • people trying to move away from this - larger strides in conversation layers
    • stacking small layers is generally better
  • most of memory impact is usually from activations from each layer kept around for backdrop
  • visualizations
    • layer activations (maybe average over channels)
    • visualize the weights (maybe average over channels)v
    • feed a bunch of images and keep track of which activate a neuron most
    • t-SNE embedding of images
    • occluding
  • weight matrices have special structure (Toeplitz or block Toeplitz)
  • input layer is usually centered (subtract mean over training set)
  • usually crop to fixed size (square input)
  • receptive field - input region
  • stride m - compute only every mth pixel
  • downsampling
    • max pooling - backprop error back to neuron w/ max value
    • average pooling - backprop splits error equally among input neurons
  • data augmentation - random rotations, flips, shifts, recolorings
  • siamese networks - extract features twice with same net then put layer on top
    • ex. find how similar to representations are

RNNs

  • feedforward NNs have no memory so we introduce recurrent NNs
  • able to have memory
  • truncated - limit number of times you unfold
  • $state_{new} = f(state_{old},input_t)$
  • ex. $h_t = tanh(W h_{t-1}+W_2 x_t)$
  • train with backpropagation through time (unfold through time)
    • truncated backprop through time - only run every k time steps
  • error gradients vanish exponentially quickly with time lag
  • LSTMS
    • have gates for forgetting, input, output
    • easy to let hidden state flow through time, unchanged
    • gate $\sigma$ - pointwise multiplication
      • multiply by 0 - let nothing through
      • multiply by 1 - let everything through
    • forget gate - conditionally discard previously remembered info
    • input gate - conditionally remember new info
    • output gate - conditionally output a relevant part of memory
    • GRUs - similar, merge input / forget units into a single update unit

graph neural networks

  • Theoretical Foundations of Graph Neural Networks
    • inputs are graphs
    • e.g. molecule input to classification
    • e.g. traffic maps - nodes are intersections
    • invariances in CNNs: translational, neighbor pixels relate a lot more
    • simplest setup: no edges, each node $i$ has a feature vector $x_i$ (really a set not a graph)
      • X is a matrix where each row is a feature vector
      • note that permuting rows of X shouldn’t change anything
      • permutation invariant: $f(PX) = f(X)$ for all permutation matrices $P$
        • e.g. $\mathbf{P}{(2,4,1,3)} \mathbf{X}=\left[\begin{array}{llll}0 & 1 & 0 & 0 \ 0 & 0 & 0 & 1 \ 1 & 0 & 0 & 0 \ 0 & 0 & 1 & 0\end{array}\right]\left[\begin{array}{lll}- & \mathbf{x}{1} & - \ - & \mathbf{x}{2} & - \ - & \mathbf{x}{3} & - \ - & \mathbf{x}{4} & -\end{array}\right]=\left[\begin{array}{lll}- & \mathbf{x}{2} & - \ - & \mathbf{x}{4} & - \ - & \mathbf{x}{1} & - \ - & \mathbf{x}_{3} & -\end{array}\right]$
        • ex. Deep Sets model (zaheer et al. ‘17): $f(X) = \phi \left (\sum_k \psi(x_i) \right)$
      • permutation equivariant: $f(PX) = P f(X)$ - useful for when we want answers at the node level
    • graph: augment set of nodes with edges between them (store as an adjacency matrix)
      • permuting permutation matrix to A requires operating on both rows and cols: $PAP^T$
      • permutation invariance: $ f\left(\mathbf{P X}, \mathbf{P A P}^{\top}\right)=f(\mathbf{X}, \mathbf{A})$
      • permutation equivariance: $f\left(\mathbf{P X}, \mathbf{P A P}^{\top}\right)=\mathbf{P} f(\mathbf{X}, \mathbf{A})$
      • can now write an equivariant function that extracts features not only of X, but also its neighbors: $g(x_b, X_{\mathcal N_b})$
        • tasks: node classification, graph classification, link (edge) prediction)
      • 3 flavors of GNN layers for extracting features from nodes / neighbors: simplest to most complex
        • message-passing actually passes vectors to be sent across edges
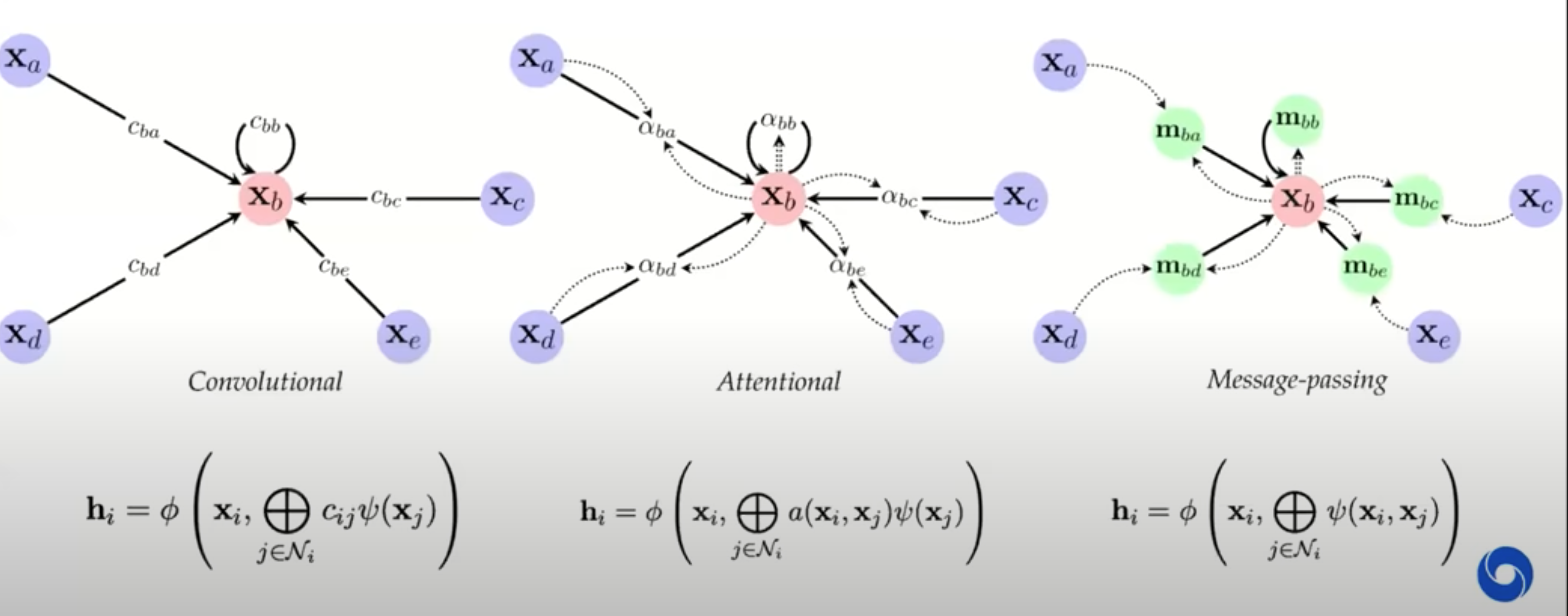
        • gnn_layers
    • previous approaches map on to gnns well
      • GNNs explicitly construct local features, much like previous works
        • local objectives: features of nodes i and j should predict existence of edge $(i, j)$
        • random-walk objectives: features should be similar if i and j co-occur on a short random walk (e.g. deepwalk, node2vec, line)
      • similarities to NLP if we think of words as nodes and sentences as walks
        • we can think of transformers as fully-connect graph networks with attentional form of GNN layers
          • one big difference: positional embeddings often used, making the input not clearly a graph
            • these postitional embeddings often take the form of sin/cos - very similar to DFT eigenvectors of a graph
      • spectral gnns
        • operate on graph laplacian matrix $L = D - A$ where $D$ is degree matrix and $A$ is adjacency matrix - more mathematically convenient
      • probabilistic modeling - e.g. assome markov random field and try to learn parameters
        • this connects well to a message-passing GNN
  • GNN limitations
    • ex. can we tell whether 2 graphs are isomorphic - often no?
    • can make GNNs more powerful by adding positional features, etc.
    • can also embed sugraphs together
    • continuous case is more difficult
  • geometric deep learning: invariances and equivariances can be applied generally to get a large calss of architectures between convolutions and graphs

misc architectural components

  • coordconv - break translation equivariance by passing in i, j coords as extra filters
  • deconvolution = transposed convolution = fractionally-strided convolution - like upsampling

top-down feedback

neural architecture search (NAS)

misc