2.5. quantum

Some very limited notes on quantum computing

• what does physics tell us about the limits of computers?

• NP - can check soln in polynomial time

• NP-hard - if solved, solves every NP

• NP-complete - NP hard and in NP

• church-turing thesis \(\implies\) turing machine polynomial time should be best possible in the universe

  • physics could allow us to do better than a turing machine

• examples

  • glass plates with soapy water - forms minimum steiner tree

  • can get stuck in local optimum

  • ex. protein folding

  • ex. relativity computer

    • leave computer on earth, travel at speed of light for a while, come back and should be done

    • if you want exponential speedup, need to get exponentially close to speed of light (requires exponential energy)

  • ex. zeno’s computer - run clock faster (exponentially more cooling = energy)

2.5.1. basics

• An n-bit computer has 2^n states and is in one of them with probability 1. You can think of it as having 2^n coefficients, one of which is 0 and the rest of which are 1. Operations on it are multiplying these coefficients by stochastic matrices. Only produces n bits of info.

• an n-qubit quantum computer is described by 2^n complex coefficients. The sum of their squares sums to 1. It’s 2^n complex coefficients must be multiplied by unitary matrices (they preserve that the sum of the squares add up to 1.)

• Problem: Decoherence – results from interaction with the outside world

• Properties:

  • Superposition – an object is in more than one state at once

    • Has a percentage of being in both states

  • Entanglement – 2 particles behave exactly the opposite – instantly

2.5.2. storing qubits

• Fullerenes – naturally found in Precambrian rock, reasonable for storing qubits – can store

  • not developed, but some experiments have shown ability to store qubits for milliseconds

2.5.3. intro

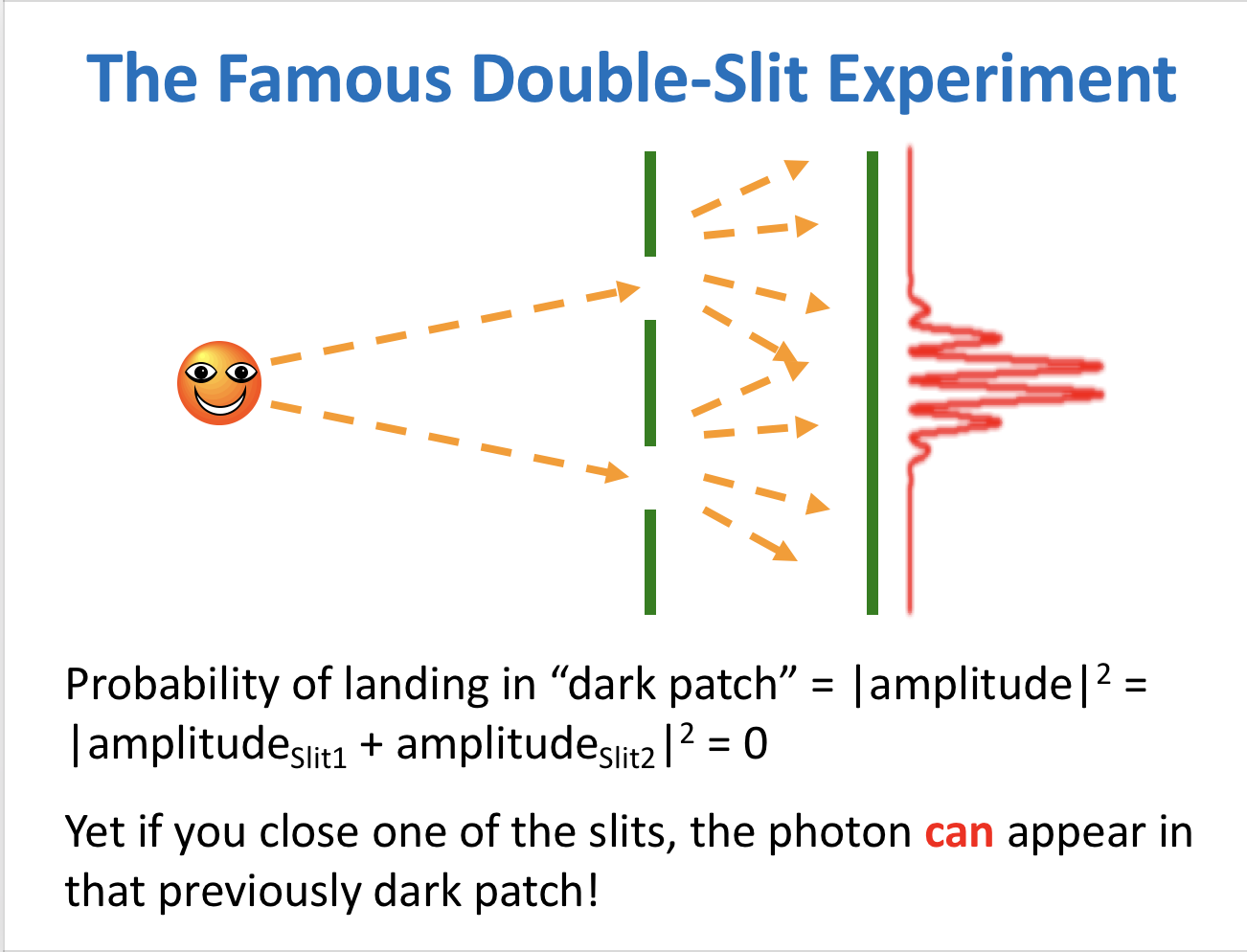
• probability with minus signs

• amplitudes - used to calculate probabilites, but can be negative / complex

• applications

  • quantum simulation

  • also could factor integers in polynomial time (shor 1994)

  • scaling up is hard because of decoherence= interaction between cubits and outside world

  • error-correcting codes can make it so we can still work with some decoherence

• algorithms

  • paths that lead to wrong answer - quantum amplitudes cancel each other out

  • for right answer, quantum amplitudes in phase (all positive or all negative)

  • prime factorization is NP but not NP complete

  • unclear that quantum can solve all NP problems

  • Grover’s algorithm - with quantum computers, something like you can only use sqrt of number of steps

  • adiabatic optimization - like quantum simulated annealing, maybe can solve NP-complete problems

• dwave - company made ~2000 cubit machine

  • don’t maintain coherence well

  • algorithms for NP-complete problems may not work

  • hope: quantum tunneling can get past local maximum in polynomial time maybe

    • empircally unclear if this is true

• quantum supremacy - getting quantum speedup for something, maybe not something useful

2.5.4. maxwell’s demon

• second law of thermodynamics: entropy is always increasing

• hot things transfer heat to cold things

  • temperature is avg kinetic energy - particles follow a diistribution of temperature

• separate 2 samples (one hot, one cold) with insulator

  • idea: demon makes all fast particles go to hot side, all slow particles go to slow side - this is against entropy

  • demon controls door between the samples

  • 

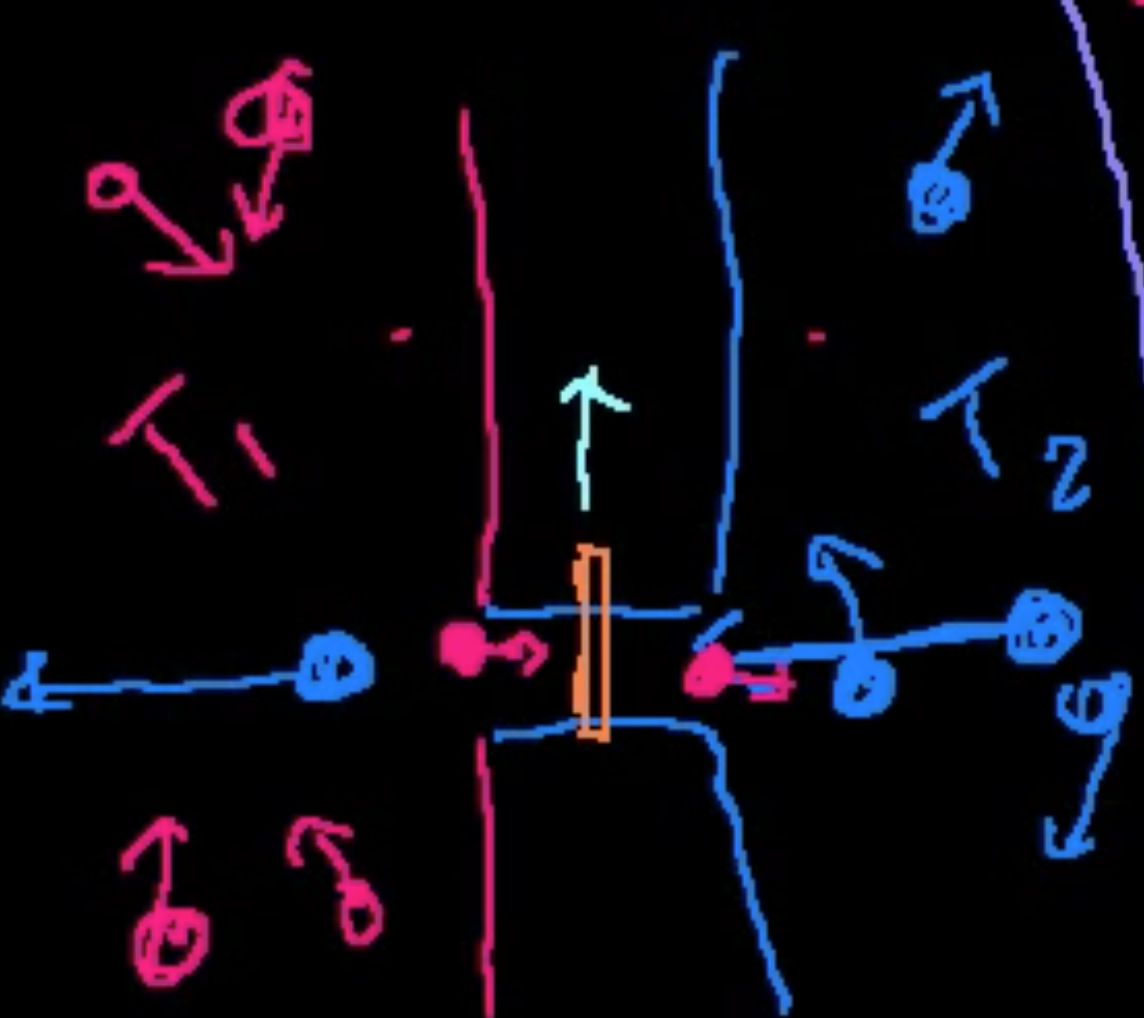
    • demon opens door whenever high temperature particle comes from cold sample, then closes

    • demon opens door for slow particles from hot sample, then closes

• problem: demon has to track all the particles (which would generate a lot of heat)

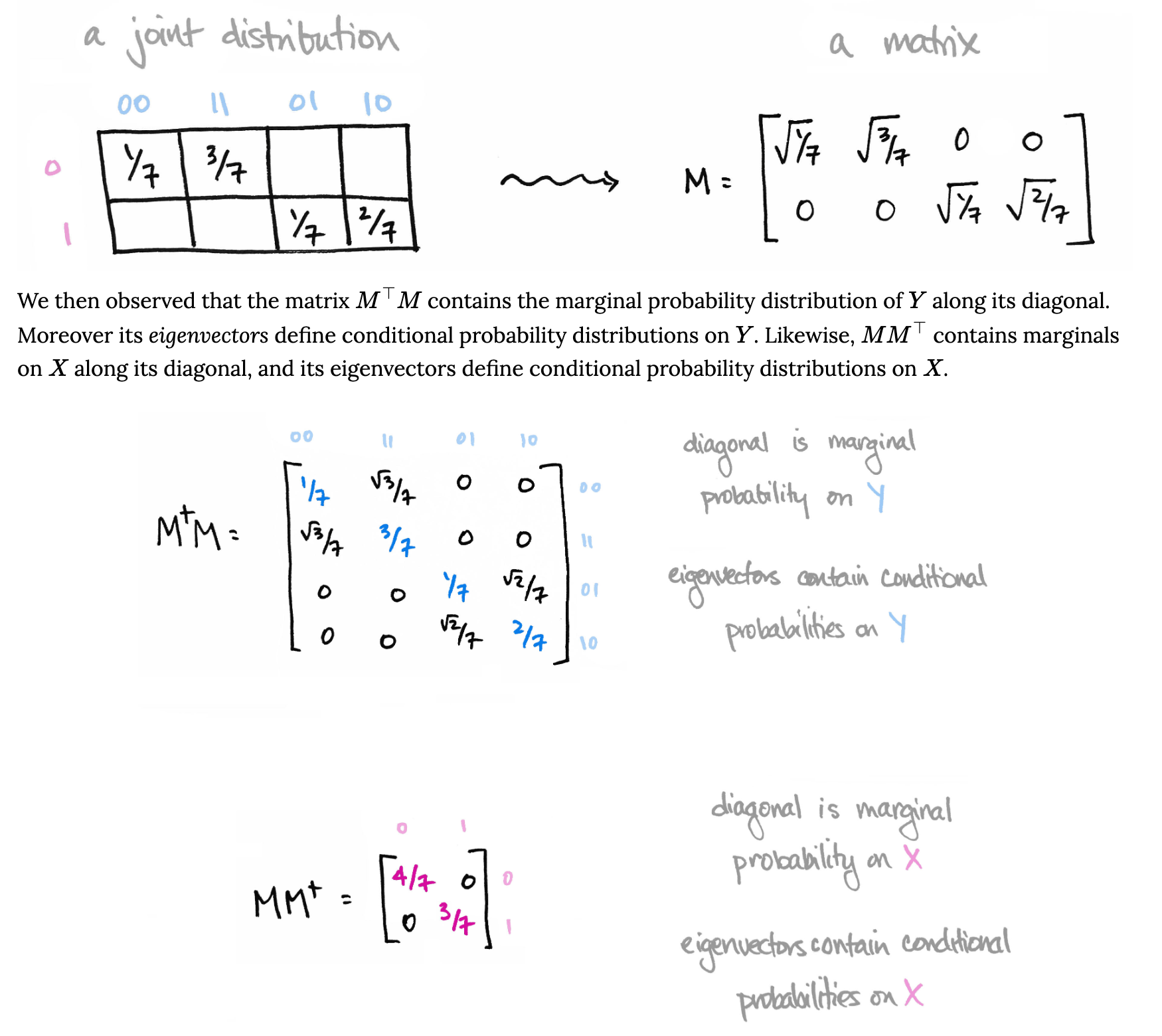
2.5.5. quantum probability

• based on this blog post

  • marginal prob. loses information but we don’t need to

•