Deep learning theory

Research overviews  ·  chapter 14 of 14  ·  15 min read

Deep learning theory#

Research directions on why deep nets generalize, from implicit regularization and kernels to statistical physics, robustness and memorization.

About this chapter

Deep nets break classical expectations: more parameters can mean better generalization, and many things (SGD, dropout, early stopping, architecture) shape what they learn all at once. The theoretical half of the page collects directions that try to separate these effects: what a net can represent, which solutions gradient descent prefers among the many that fit the data, why parameters are redundant, how infinitely wide nets reduce to kernels, rewriting nets as implicit or constrained optimization problems, and analyses from statistical physics.

The empirical half covers the lottery ticket hypothesis, adversarial robustness, tools for looking at trained nets, and memorization, with shorter lists on optimizers, architecture search and boosting. The “inductive bias” and “kernels” sections are the best place to start; the basics section at the end lists class notes and demos.

off convex blog

Theoretical studies#

The open questions behind the rest of the page: what happens past the point where training error stops falling, what marks a well-trained net, and how to tell which of the many tangled ingredients actually drive generalization.

DNNs display many surprising properties

  • surprising: more parameters yields better generalization (novak et al. 2018)

  • surprising: lowering training error should be harder

Many things seem to contribute to the inductive bias of DNNs: SGD, dropout, early stopping, resnets, convolution, more layers…all of these are tangled together and many things correlate with generalization error…what are the important things and how do they contribute?

some more concrete questions:

  • what is happening when training err stops going down but val err keeps going down (interpolation regime)?

  • what are good statistical markers of an effectively trained DNN?

  • how far apart are 2 nets?

  • verification - does dnn satisfy a specification (e.g \(l_p\) robustness)

    • convex barrier - limitation in the tightness of the bounds obtainable by the convex relaxation of the output of a neural network

Functional approximation#

Studying nets as functions rather than as parameters, since many parameter settings give the same function. With composition, a net can approximate a function piece by piece on its level sets.

  • dnns are very hard to study in the parameter space (e.g. swapping two parameters changes things like the Hessian), easier to to study in the function space (e.g. the input-output relationship)

  • nonlinear approximation (e.g. sparse coding) - 2 steps

  1. construct a dictionary function (T)

  2. learn linear combination of the dictionary elements (g)

  • background

    • \(L^2\) function (or function space) is square integrable: \(\vert f\vert ^2 = \int_X \vert f\vert ^2 d\mu\), and \(\vert f\vert\) is its \(L_2\)-norm

    • Hilbert space - vector space w/ additional structure of inner product which allows length + angle to be measured

      • complete - there are enough limits in the space to allow calculus techniques (is a complete metric space)

  • composition allows an approximation of a function through level sets (split it up and approximate on these sets) - Zuowei Shen (talk, slides)

    • composition operation allows an approximation of a function f through level sets of f –

    • one divides up the range of f into equal intervals and approximate the functions on these sets

    • nonlinear approximation via compositions (shen 2019)

  • how do the weights in each layer help this approximation to be more effective?

    • here are some thoughts – If other layers are like the first layer, the weights “whiten” or make the inputs more independent or random projections – that is basically finding PC directions for low-rank inputs.

    • are the outputs from later layers more or less low - rank?

    • I wonder how this “whitening” helps level set estimation…

  • takagi functions

  • nonlinear approximation and (deep) relu nets - also comes with slides

Inductive bias=implicit regularization: gradient descent finds good minima#

Among the many solutions that fit the training data, gradient descent tends to find particular ones. The simplest case is least squares started at 0: gradient descent stays in the row space of \(X\) and converges to the minimum-norm solution, the same endpoint as ridge as \(\lambda \to 0\). The examples that follow find the matching norm for matrix completion, logistic regression and convolutional nets.

Interactive 1. Least squares with one data point and two weights: every point on the blue line fits exactly. Each gradient step moves along \(a\), the row space of \(X\), so from \(w_0 = 0\) gradient descent stops at the min-norm solution \(w^*\), inside the dashed circle that every other solution lies outside of. Move \(w_0\) off zero: the limit shifts by the part of \(w_0\) outside the row space and its norm grows. Step \(t\) forward and compare with the ridge solution at \(\lambda = 1/(\eta t)\), which runs along the same ray.

DL learns solutions that generalize even though it can find many which don’t due to its inductive bias.

  • gd bousquet paper (maennel et al. 2018)

  • in high dims, local minima are usually saddles (ganguli)

  • early stopping is very similar to ridge regression

  • ridge regression: soln will lie in \(p-dim\) row-space of X (span of the rows)

    • when \(\lambda \to 0\), will give us min-norm soln (basically because we project onto \(col(X)\))

    • early stopping in least squares

      • if we initialize at 0, GD soln will always be in the row-space of X

      • GD will converge to min-norm soln (any soln not in the row-space will necessarily have larger norm)

      • similar to ridge (endpoints are the same) and can related their risks very closely when \(\lambda = 1/t\), where \(t\) is GD time iterate

        • assume gradient flow: take step-size to 0

  • srebro understanding over-parameterization (neyshabur et al. 2018)

    • ex. gunasekar et al 2017: unconstrained matrix completion

      • grad descent on U, V yields min nuclear norm solution

    • ex. soudry et al 2017

      • sgd on logistic reg. gives hard margin svm

      • deep linear net gives the same thing - doesn’t actually changed anything

    • ex. gunaskar, 2018

    • ex. savarese 2019

      • infinite width relu net 1-d input

      • weight decay minimization minimizes derivative of TV

  • implicit bias towards simpler models (valle-pérez et al. 2018)

  • How do infinite width bounded norm networks look in function space? (savarese…srebro 2019)

    • minimal norm fit for a sample is given by a linear spline interpolation (2 layer net)

  • analytic theory of generalization + transfer (ganguli 19) (lampinen & ganguli 2018)

    • deep linear nets learn important structure of the data first (less noisy eigenvectors)

    • similar paper for layer nets (gidel et al. 2019)

  • datasets for measuring causality

    • Inferring Hidden Statuses and Actions in Video by Causal Reasoning - about finding causality in the video, not interpretation

  • PL condition = Polyak-Lojawsiewicz condition guarantees global convergence of loca methods

    • \(\vert \vert \nabla f(x)\vert \vert ^2 \geq \alpha f(x) \geq 0\)

Semantic biases: what correlations will a net learn?#

Which features a trained net ends up using, for example texture over shape on ImageNet, and what pushes it toward simpler or spurious ones.

  • imagenet models are biased towards texture (geirhos et al. 2018) (and removing texture makes them more robust)

  • analyzing semantic robustness (hamdi & ghanem 2019)

  • eval w/ simulations (oramas et al. 2017) (reviewer argued against this)

  • glcm captures superficial statistics (wang et al. 2019)

  • deeper, unpruned networks are better against noise (hendrycks & dietterich 2019)

  • analytic theory of generalization + transfer (ganguli 19) (lampinen & ganguli 2018)

  • causality in dnns talk by bottou

    • on mnist, color vs shape will learn color

  • A mathematical theory of semantic development in deep neural networks (saxe et al. 2018)

  • rl agents learn some crazy things (lehman et al. 2018)

  • Emergence of Invariance and Disentanglement in Deep Representations (achille & soatto 2018)

    • information in the weights as a measure of complexity of a learned model (information complexity)

    • IB Lagrangian between the weights of a network and the training data, as opposed to the traditional one between the activations and the test datum

    • explains tradeoff between over/underfitting

  • On Dropout, Overfitting, and Interaction Effects in Deep Neural Networks (lengerich..caruana, 2020)

    • use ANOVA to meaure 1st/2nd/3rd order effects and such

      • approximate ANOVA decomp. using boosted trees of depth based on a particular order

  • they find that increasing dropout rate forces nets to emphasize lower-order effects

  • An Investigation of Why Overparameterization Exacerbates Spurious Correlations (sagawa et al. 2020)

    • overparameterization can hurt test error on minority groups despite improving average test error when there are spurious correlations in the data

Expressiveness: what can a dnn represent?#

A ReLU net is piecewise linear, so one measure of what it can represent is how many linear regions and activation patterns it has. These papers count and bound them; trained nets turn out to use fewer than the maximum.

Complexity + generalization: dnns are low-rank / redundant parameters#

Evidence that trained nets need far fewer parameters than they have: low-rank weight matrices, pruning, and lottery tickets that train well at a small fraction of the size.

Nearest neighbor comparisons#

Nearest neighbor rules that interpolate the training data can still generalize, which makes them a simple reference point for nets that also fit the training set exactly.

Kernels#

In the infinite-width limit a randomly initialized net is a Gaussian process with a fixed kernel, and training follows the neural tangent kernel, which barely changes during training. Gradient descent in kernel space can be convex even when the problem is non-convex in parameter space.

  • To understand deep learning we need to understand kernel learning (belkin et al. 2018) - overfitted kernel classifiers can still fit the data well

  • original kernels (neal 1994) + (lee et al. 2018) + (matthews et al. 2018)

    • infinitely wide nets and only top layer is trained

    • corresponds to kernel \(\text{ker}(x, x') = \mathbb E_{\theta \sim W}[f(\theta, x) \cdot f(\theta, x')]\), where \(W\) is an intialization distr. over \(\theta\)

  • neural tangent kernel (jacot et al. 2018)

    • \(\text{ker}(x, x') = \mathbb E_{\theta \sim W} \left[\left < \frac{f(\theta, x)}{\partial \theta} \cdot \frac{f(\theta, x')}{\partial \theta} \right> \right]\) - evolution of weights over time follows this kernel

      • with very large width, this kernel is the NTK at initialization

      • stays stable during training (since weights don’t change much)

    • at initialization, artificial neural networks (ANNs) are equivalent to Gaussian processes in the infinite-width limit

      • evolution of an ANN during training can also be described by a kernel (kernel gradient descent)

    • different types of kernels impose different things on a function (e.g. want more / less low frequencies)

      • gradient descent in kernel space can be convex if kernel is PD (even if nonconvex in the parameter space)

    • understanding the neural tangent kernel (arora et al. 2019)

      • method to compute the kernel quickly on a gpu

  • Scaling description of generalization with number of parameters in deep learning (geiger et al. 2019)

    • number of params = N

    • above 0 training err, larger number of params reduces variance but doesn’t actually help

      • ensembling with smaller N fixes problem

    • the improvement of generalization performance with N in this classification task originates from reduced variance of fN when N gets large, as recently observed for mean-square regression

  • On the Inductive Bias of Neural Tangent Kernels (bietti & mairal 2019)

  • Kernel and Deep Regimes in Overparametrized Models (woodworth…srebro 2019)

    • transition between kernel and deep regimes

  • The HSIC Bottleneck: Deep Learning without Back-Propagation (ma et al. 2019)

    • directly optimize information bottleneck (approximated by HSIC) yields pretty good results

Random projections#

Implicit dl + optimization#

Rewriting a net as an optimization problem. Implicit models define the hidden state by the equation \(x = \phi(\cblue{Ax + Bu})\), and a feedforward net is the special case where \(A\) holds the weight matrices just above its diagonal. Lifted nets turn each layer into a constraint. The robust optimization entries that follow make guarantees hold under worst-case perturbations.

  • implicit deep learning (el ghaoui et al. 2019)

    • \(\hat y (u) = \corange{Cx + D u} \), where \(x = \phi(\cblue{Ax + Bu})\)

      • here, \(u\) is a new input

      • \(x\) is a hidden state which represents some hidden features (which depends on \(u\))

        • well-posedness - want x to be unique for a given u

      • \(\cblue{A, B}\) are matrices which let us compute \(x\) given \(u\)

      • \(\corange{C, D}\) help us do the final prediction (like the final linear layer)

    • ex. feedforward nets

      • consider net with \(L\) layers

        • \(x_0 = u\)

        • \(x_{l + 1} = \phi_l (W_l x_l)\)

        • \(\hat y (u) = W_L x_L\)

      • rewriting in implicit form

        • \(x = (x_L, ..., x_1)\) - concatenate all the activations into one big vector

        • matrix form

          \[\begin{split} \left(\begin{array}{c|c} \cblue{A} & \cblue{B} \\ \hline \corange{C} & 0 \end{array}\right) = \left(\begin{array}{cccc|c} 0 & W_{L-1} & \cdots & 0 & 0 \\ & 0 & \ddots & \vdots & \vdots \\ & & \ddots & W_1 & 0 \\ & & & 0 & W_0 \\ \hline W_L & 0 & \cdots & 0 & 0 \end{array}\right) \end{split}\]

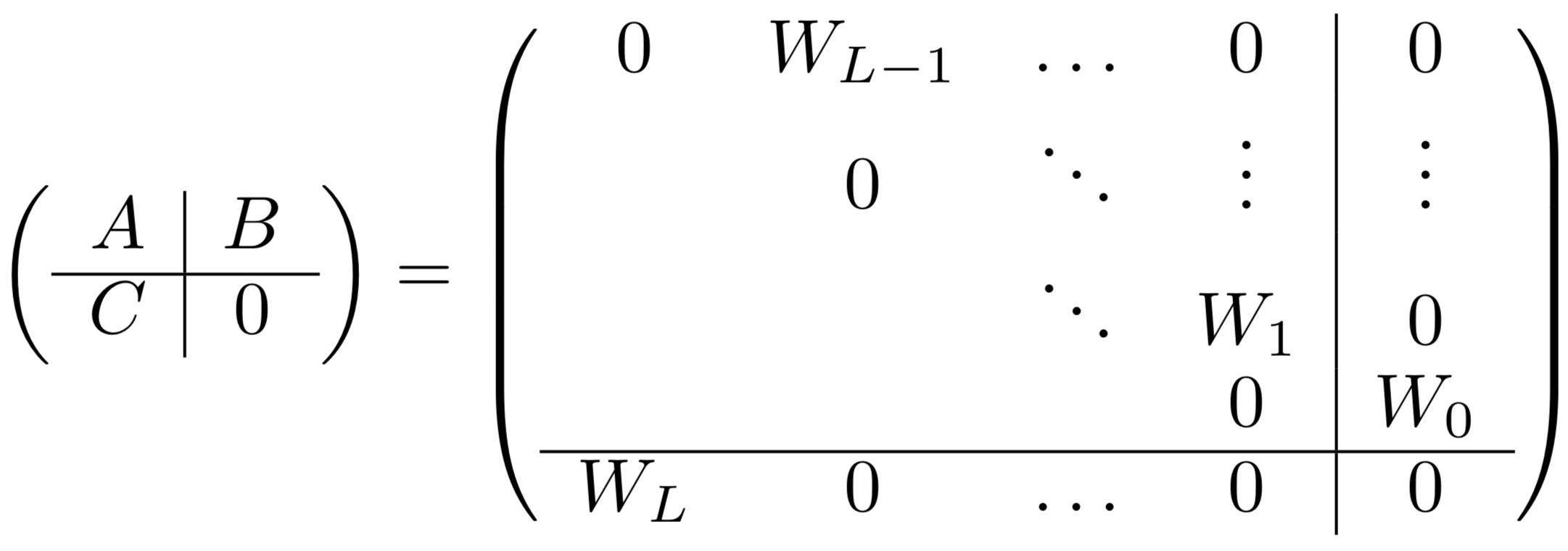
        • ex. \(Ax + Bu= \begin{bmatrix} W_{L-1}x_{L-1} \\ W_{L-2} x_{L-2} \\ \vdots \\ W_1x_1 \\ \mathbf 0\end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ W_0 u \end{bmatrix}\)

  • lifted neural networks (askari et al. 2018)

    • can solve dnn \(\hat y = \phi(W_2 \phi (W_1X_0))\) by rewriting using constraints:

      • \(X_1 = \phi(W_1 X_0)\)

      • \(X_2 = \phi(W_2 X_1)\)

    • \[\begin{split}\begin{align} &\min \cblue{(y - \hat y)^2}\\s.t. \corange{X_1} &\corange{ {}= \phi(WX_0)}\\\corange{X_2} &\corange{ {}= \phi(WX_1)}\end{align}\end{split}\]

    • can be written using Lagrangian multipliers: \(\min \cblue{(y - \hat y)^2} + \corange{\lambda_1( X_1 - \phi(WX_0)) + \lambda_2(X_2 - \phi(WX_1))}\)

      • loss + constraint terms

  • Fenchel Lifted Networks: A Lagrange Relaxation of Neural Network Training (gu et al. 2018)

    • in the lifted setting above, can replace Lagrangian with simpler expression using Fenchel conjugates

  • robust optimization basics

    • immunize optimization problems against uncertainty in the data

    • do so by having worst-case constraints (e.g. \(a < 5, \forall a\))

    • local robustness - maximize radius surrounding parameter subject to all constraints (no objective to maximize)

    • global robustness - maximize objective subject to robustness constraint (trades off robustness with objective value)

    • non-probabilistic robust optimization models (e.g. Wald’s maximin model: \(\underset{x}{\max} \underset{u}{\min} f(x, u)\)

    • also are probabilistically robust optimization

  • distributional robustness - using moments in the dl work

    • ch 4 and ch10 of robust optimization book (bental, el ghaoui, & nemirovski 2009)

    • Certifying Some Distributional Robustness with Principled Adversarial Training (sinha, namkoong, & duchi 2018)

      • want to guarantee performance under adversarial input perturbations

      • considering a Lagrangian penalty formulation of perturbing the underlying data distribution in a Wasserstein ball

        • during training, augments model parameter updates with worst-case perturbations of training data

      • little extra cost and achieves guarantees for smooth losses

    • On Distributionally Robust Chance-Constrained Linear Programs (calafiore & el ghaoui 2006)

      • linear programs where data (in the constraints) is random

      • want to enforce the constraints up to a given prob. level

      • can convert the prob. constraints into convex 2nd-order cone constraints

      • under distrs. for the random data, can guarantee constraints

  • Differentiable Convex Optimization Layers (agrawal et al. 2019)

Statistical physics#

Ideas from physics applied to depth, initialization and generalization bounds. Generalization bounds usually have the form train error + complexity term, and the physics view adds alternatives such as stability and symmetry-based conservation laws.

  • Statistical Mechanics of Deep Learning (bahri et al. 2019)

    • what is the advantage of depth - connect to dynamical phase transitions

      • there are several function which require only polynomial nodes in each layer for deep nets, but exponential for shallow nets

    • what is the shape of the loss landscape - connect to random Gaussian processes, sping glasses, and jamming

    • how to pick a good parameter initialization?

    • bounding generalization error

      • often, generalization bounds take the form \(\epsilon_{test} \leq \cblue{\epsilon_{train}} + \corange{\frac {\mathcal C (\mathcal F)} p}\) (train error + complexity term), where \(\mathcal C (\mathcal F)\) is the complexity of a function class and \(p\) is the number of examples

        • ex. VC-dimension, Rademacher complexity

      • alternative framework: algorithmic stability - will generalize if map is stable wrt perturbations of the data \(\mathcal D\)

      • altenative: PAC bounds suggest if distr. of weights doesn’t change much during training, generalization will be succesful

    • deep linear networks

      • student learns biggest singular values of the input-output correlation matrix \(\Sigma = \sum_i y_i x_i^T\), so it learns the important stuff first and the noise last

    • infinite-width limit

      • if parameters are random, indcues a prior distribution \(P(\mathcal F)\) over the space of functions

      • in th limit of infinite width, this prior is Gaussian, with a specific correlation kernel

      • learning is similar to learning the Bayesian posterior \(P(f\vert data)\), but connecting this to sgd is still not clear

  • Neural Mechanics: Symmetry and Broken Conservation Laws in Deep Learning Dynamics (kunin et al. 2020)

    • no assumptions about DNN architecture or gradientflow

    • instead, assumptions on symmetries embedded in a network’s architecture constrain training dynamics

      • similar to Noether’s thm in physics

    • can much better analytically describe learning dynamics

    • weights have a differentiable symmetry in the loss if the loss doesn’t change under a certain differentiable transformation of the weights

      • ex. translation symmetry - for layer before softmax, we get symmetries across weights that shift all outputs

      • ex. scale symmetry - inputs to batch normalization are invariant to scaling

      • ex. rescale symmetry - scaling up/down 2 things which multiply or add

    • modeling discretization

Empirical studies#

Experiments rather than theorems. Many of these probe a claim from the theory half, for example whether nets memorize, which layers matter, or how robustness trades off with accuracy.

Interesting empirical papers#

The lottery ticket hypothesis is the main entry: large nets that train well contain small subnetworks that train as well on their own. The others test robustness to label noise, which layers matter, and whether theoretical claims hold up in practice.

Adversarial + robustness#

Attacks are sorted by what the attacker knows (white, gray or black box) and when they act (poisoning at training time or evasion at test time). Defenses either mask gradients, train against worst-case inputs, or detect attacks. The later entries move from single inputs to robustness across groups and domains.

  • robustness may be at odds with accuracy (madry 2019)

    • adversarial training helps w/ little data but hurts with lots of data

    • adversarially trained models have more meaningful gradients (and their adversarial examples actually look like other classes)

  • Generalizability vs. Robustness: Adversarial Examples for Medical Imaging (paschali et al. 2018)

  • Towards Robust Interpretability with Self-Explaining Neural Networks (alvarez-melis & jaakkola 2018)

  • Adversarial Attacks and Defenses in Images, Graphs and Text: A Review (xu et al. 2019)

    • Adversarial examples are inputs to machine learning models that an attacker intentionally designed to cause the model to make mistakes

    • threat models

      • poisoning attack (insert fake samples into training data) vs. evasion attack (just evade at test time)

      • targeted attack (want specific class) vs. non-targeted attack (just change the prediction)

    • adversary’s knowledge

      • white-box - adversary knows everything

      • black-box - can only feed inputs and get outputs

      • gray-box - might have white box for limited amount of time

    • security evaluation

      • robustness - minimum norm perturbation to change class

      • adversarial loss - biggest change in loss within some epsilon ball

    • attacks

      attack

      publication

      similarity

      attacking capability

      algorithm

      apply domain

      L-BFGS

      (Szegedy et al., 2013)

      \(l_2\)

      White-Box

      Iterative

      Image Classification

      FGSM

      (Goodfellow et al., 2014b)

      \(l_\infty, l_2\)

      White-Box

      Single-Step

      Image Classification

      Deepfool

      (Moosavi-Dezfooli et al., 2016)

      \(l_2\)

      White-Box

      Iterative

      Image Classification

      JSMA

      (Papernot et al., 2016a)

      \(l_2\)

      White-Box

      Iterative

      Image Classification

      BIM

      (Kurakin et al., 2016a)

      \(l_\infty\)

      White-Box

      Iterative

      Image Classification

      C & W

      (Carlini & Wagner, 2017b)

      \(l_2\)

      White-Box

      Iterative

      Image Classification

      Ground Truth

      (Carlini et al., 2017)

      \(l_0\)

      White-Box

      SMT solver

      Image Classification

      Spatial

      (Xiao et al., 2018b)

      Total Variation

      White-Box

      Iterative

      Image Classification

      Universal

      (Metzen et al., 2017b)

      \(l_\infty, l_2\)

      White-Box

      Iterative

      Image Classification

      One-Pixel

      (Su et al., 2019)

      \(l_0\)

      White-Box

      Iterative

      Image Classification

      EAD

      (Chen et al., 2018)

      \(l_1 + l_2, l_2\)

      White-Box

      Iterative

      Image Classification

      Substitute

      (Papernot et al., 2017)

      \(l_p\)

      Black-Box

      Iterative

      Image Classification

      ZOO

      (Chen et al., 2017)

      \(l_p\)

      Black-Box

      Iterative

      Image Classification

      Biggio

      (Biggio et al., 2012)

      \(l_2\)

      Poisoning

      Iterative

      Image Classification

      Explanation

      (Koh & Liang, 2017)

      \(l_p\)

      Poisoning

      Iterative

      Image Classification

      Zugner’s

      (Zügner et al., 2018)

      Degree Distribution, Coocurrence

      Poisoning

      Greedy

      Node Classification

      Dai’s

      (Dai et al., 2018)

      Edges

      Black-Box

      RL

      Node & Graph Classification

      Meta

      (Zügner & Günnemann, 2019)

      Edges

      Black-Box

      RL

      Node Classification

      C & W

      (Carlini & Wagner, 2018)

      max dB

      White-Box

      Iterative

      Speech Recognition

      Word Embedding

      (Miyato et al., 2016)

      \(l_p\)

      White-Box

      One-Step

      Text Classification

      HotFlip

      (Ebrahimi et al., 2017)

      letters

      White-Box

      Greedy

      Text Classification

      Jia & Liang

      (Jia & Liang, 2017)

      letters

      Black-Box

      Greedy

      Reading Comprehension

      Face Recognition

      (Sharif et al., 2016)

      physical

      White-Box

      Iterative

      Face Recognition

      RL attack

      (Huang et al., 2017)

      \(l_p\)

      White-Box

      RL

    • defenses

      • gradient masking

        • shattered gradient: (Buckman et al., 2018), (Guo et al., 2017)

        • shattered gradient: (Dhillon et al., 2018), (Xie et al., 2017a)

        • exploding/vanishing gradient: (Song et al., 2017), (Samangouei et al., 2018), (Papernot et al., 2016b)

      • robust optimization

        • adversarial training: (Goodfellow et al., 2014b), (Madry et al., 2017), (Tramèr et al., 2017), (Sinha et al., 2017)

        • certified defense: (Wong & Kolter, 2017), (Hein & Andriushchenko, 2017), (Raghunathan et al., 2018a), (Sinha et al., 2017)

        • regularization: (Cisse et al., 2017), (Gu & Rigazio, 2014), (Rifai et al., 2011)

      • detection

        • auxiliary model: (Grosse et al., 2016), (Gong et al., 2017), (Metzen et al., 2017a)

        • statistical methods: (Hendrycks & Gimpel, 2016), (Grosse et al., 2017), (Gretton et al., 2012)

        • check consistency: (Feinman et al., 2017), (Xu et al., 2017)

  • AugMix: A Simple Data Processing Method to Improve Robustness and Uncertainty (hendrycks et al. 2020)

    • do a bunch of transformations and average images to create each training image

  • certifying robustness

    • bound gradients of f around x - solve SDP for 2-layer net (raghunathan, steinhardt, & liang 2018, iclr)

      • relax SDP and then applies to multilayer nets (raghunathan et al. 2018)

      • improved optimizer for the SDP (dathathri et al. 2020)

    • interval bound propagation - instead of passing point, pass an interval where it could be

      • works well for word substitions (jia et al. 2019)

    • RobEn - cluster words that are confusable + give them the same encoding when you train (jones et al. 2020)

      • then you are robust to confusing the words

  • unlabeled data + self-training helps

    • training robust models has higher sample complexity than training standard models

    • tradeoff between robustness and accuracy (raghunathann et al. 2020)

      • adding valid data can hurt even in well-specified, convex setting

      • robust self-training eliminates this tradeoff in linear regression

    • sample complexity can be reduced with unlabeled examples (carmon et al. 2019)

  • distributional robust optimization

    • instead of minimizing training err, minimize maximum training err over different perturbations

    • hard to pick the perturbation set - can easily be too pessimistic

    • these things possibly magnify disparities

      • larger models

      • selective classification

      • feature noise

      • removing spurious features

    • group DRO (sagawa et al. 2020) - maximize error for worst group

      • need to add regularization to keep errors from going to 0

      • training overparameterized models makes this problem worse

    • abstain from classifying based on confidence (jones et al. 2020)

      • makes error rates worse for worst group = selective classification can magnify disparities

    • adding feature noise to each group can magnify disparities

  • domain adaptation

    • standard domain adaptation: labeled (x, y) in source and unlabeled x in target

    • gradual domain adaptation - things change slowly over time, can use gradual self-training (kumar et al. 2020)

    • In-N-Out (xie et al. 2020) - if we have many features, rather than using them all as features, can use some as features and some as targets when we shift, to learn the domain shift

Tools for analyzing#

Ways to look inside trained nets: comparing representations with SVCCA, and plotting the loss along a line or on a 2d grid of directions. Loss plots need care with scale invariance, so directions are normalized per filter.

  • dim reduction: svcca, diffusion maps

  • viz tools: bei wang

  • visualizing loss landscape (li et al. 2017)

  • 1d: plot loss by extrapolating between 2 points (start/end, 2 ends)

    • goodfellow et al. 2015, im et al. 2016

    • exploring landscape with this technique (draxler et al. 2018)

    • 2d: plot loss on a grid in 2 directions

    • important to think about scale invariance (dinh et al. 2017)

    • want to scale direction vector to have same norm in each direction as filter

    • use PCA to find important directions (ex. sample w at each step, pca to find most important directions of variance)

Misc theoretical areas#

Comparing representations#

Simple papers#

Adam vs sgd#

A short list on whether the optimizer changes what is learned: the regularization SGD imposes (balanced layers), the limited value of adaptive methods, and a mean-field view of training.

Memorization background#

How nets that fit random labels differ from nets that generalize. Nets that generalize are close to linear in deep layers for similar inputs; nets that memorize are not.

  • memorization on single training example (zhang et al. 2019)

  • memorization in dnns (arpit et al. 2017)

  • “memorization” as the behavior exhibited by DNNs trained on noise, and conduct a series of experiments that contrast the learning dynamics of DNNs on real vs. noise data

    • look at critical samples - adversarial exists nearby

  • networks that generalize well have deep layers that are approximately linear with respect to batches of similar inputs

    • networks that memorize their training data are highly non-linear with respect to similar inputs, even in deep layers

    • expect that with respect to a single class, deep layers are approximately linear

  • example forgetting paper

  • secret sharing

  • memorization in overparameterized autoencoders (radhakrishnan et al. 2018)

    • autoencoders don’t lean identity, but learn projection onto span of training examples = memorization of training examples

    • sometimes output individual training images, not just project onto space of training images

  • https://arxiv.org/pdf/1810.10333.pdf

  • https://arxiv.org/pdf/1909.12362.pdf

  • https://pdfs.semanticscholar.org/a624/6278cb5e2d0ab79fe20fe20a41c586732a11.pdf

  • Auto-encoders: reconstruction versus compression

Probabilistic inference#

Architecture search background#

Three ways to search for an architecture: retrain each candidate (nested), make the choice differentiable (joint), or train one large net and search for a subnet in it (one-shot), the last of which connects back to pruning and lottery tickets.

Bagging and boosting#

Basics#

Starting points rather than research papers: class notes, interactive demos for building intuition, and reviews of the theory.

Key ideas

  • The central puzzle is why overparameterized nets generalize when they could fit noise, and which of the tangled ingredients (SGD, architecture, early stopping, dropout) is responsible.

  • Implicit regularization is one answer. Among the solutions that fit the data, gradient descent finds particular ones, such as the minimum-norm solution for least squares started at 0.

  • In the infinite-width limit nets reduce to kernels (a Gaussian process at initialization, the neural tangent kernel during training), and the open question is how far trained nets depart from this regime.

  • Trained nets are highly redundant (low-rank weights, pruning, lottery tickets), which links parameter count, effective complexity and generalization.

  • Empirical work tests these ideas and adds its own threads, such as adversarial robustness and its trade-off with accuracy, memorization of random labels, and tools for viewing loss surfaces and representations.

Contents