deep learning

3.4. deep learning#

See also notes in 📌 unsupervised learning, 📌 disentanglement, 📌 nlp, 📌 transformers

3.4.1. historical top-performing nets#

  • LeNet (1998)

    • first, used on MNIST

  • AlexNet (2012)

    • landmark (5 conv layers, some pooling/dropout)

  • ZFNet (2013)

    • fine tuning and deconvnet

  • VGGNet (2014)

    • 19 layers, all 3x3 conv layers and 2x2 maxpooling

  • GoogLeNet (2015)

    • lots of parallel elements (called Inception module)

  • Msft ResNet (2015)

    • very deep - 152 layers

      • connections straight from initial layers to end

      • only learn “residual” from top to bottom

  • Region Based CNNs (R-CNN - 2013, Fast R-CNN - 2015, Faster R-CNN - 2015)

    • object detection

  • Generating image descriptions (Karpathy , 2014)

    • RNN+CNN

  • Spatial transformer networks (2015)

    • transformations within the network

  • Segnet (2015)

    • encoder-decoder network

  • Unet (Ronneberger, 2015)

    • applies to biomedical segmentation

  • Pixelnet (2017) - predicts pixel-level for different tasks with the same architecture - convolutional layers then 3 FC layers which use outputs from all convolutional layers together

  • Squeezenet

  • Yolonet

  • Wavenet

  • Densenet

  • NASNET

  • Efficientnet (2019)

3.4.2. basics#

  • basic perceptron update rule

    • if output is 0, label is 1: increase active weights

    • if output is 1, label is 0: decrease active weights

  • perceptron convergence thm - if data is linearly separable, perceptron learning algorithm wiil converge

  • transfer / activation functions

    • sigmoid(z) = \(\frac{1}{1+e^{-x}} = \frac{e^x}{e^x+1}\)

    • Binary step

    • TanH (preferred to sigmoid)

    • Rectifier = ReLU

      • Leaky ReLU - still has some negative slope when <0

      • rectifying in electronics converts analog -> digital

    • rare to mix and match neuron types

  • deep - more than 1 hidden layer

  • mean-squared error (regression loss) = \(\frac{1}{2}(y-\hat{y})^2\)

  • cross-entropy loss (classification loss) = \(=-\sum_j y_j \ln \hat{p}_j\)

    • for binary classification, \(y_j\) would take on 0 or 1 and \(\hat y_j\) would be a probability

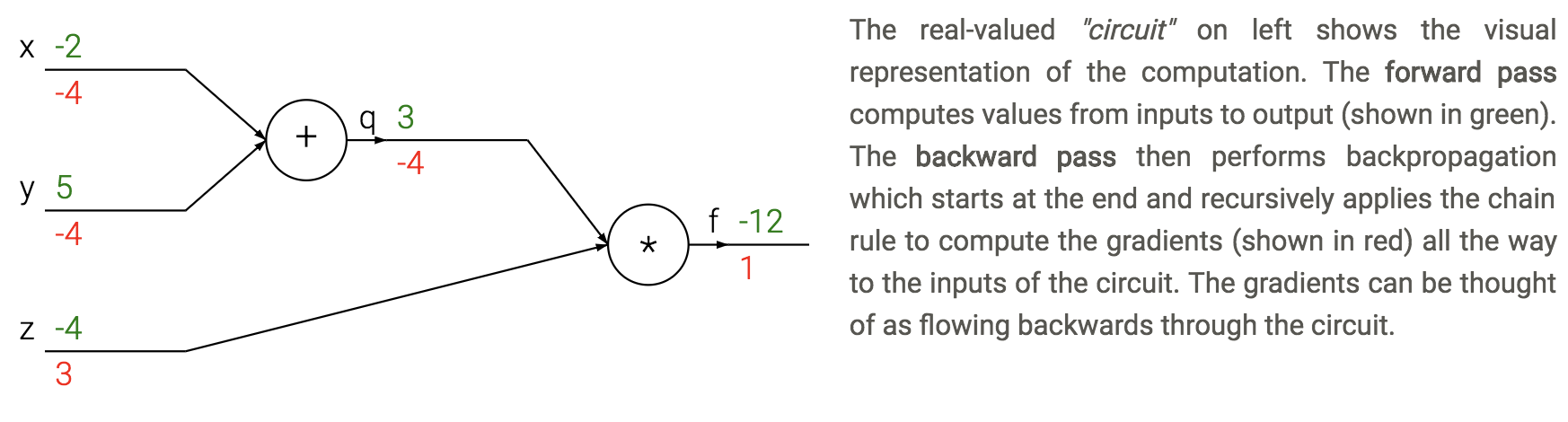
  • backpropagation - application of reverse mode automatic differentiation to neural networks’s loss

    • apply the chain rule from the end of the program back towards the beginning

      • \(\frac{dL}{d \theta_i} = \frac{dL}{dz} \frac{\partial z}{\partial \theta_i}\)

      • sum \(\frac{dL}{dz}\) if neuron has multiple outputs z

      • L is output

    • \(\frac{\partial z}{\partial \theta_i}\) is actually a Jacobian (deriv each \(z_i\) wrt each \(\theta_i\) - these are vectors)

      • each gate usually has some sparsity structure so you don’t compute whole Jacobian

  • pipeline

    • initialize weights, and final derivative (\(\frac{dL}{dL}=1\))

    • for each batch

      • run network forward to compute outputs at each step

      • compute gradients at each gate with backprop

      • update weights with SGD

  • backprop

3.4.3. training#

  • vanishing gradients problem - neurons in earlier layers learn more slowly than in later layers

    • happens with sigmoids

    • dead ReLus

  • exploding gradients problem - gradients are significantly larger in earlier layers than later layers

    • RNNs

  • batch normalization - whiten inputs to all neurons (zero mean, variance of 1)

    • do this for each input to the next layer

  • dropout - randomly zero outputs of p fraction of the neurons during training

    • like learning large ensemble of models that share weights

    • 2 ways to compensate (pick one)

      1. at test time multiply all neurons’ outputs by p

      2. during training divide all neurons’ outputs by p

  • softmax - takes vector z and returns vector of the same length

    • makes it so output sums to 1 (like probabilities of classes)

  • tricks to squeeze out performance

    • ensemble models

    • (stochastic) weight averaging can help a lot

    • test-time augmentation

      • this could just be averaging over dropout resamples as well

    • gradient checkpointing (2016 paper)

      • 10x larger DNNs into memory with 20% increase in comp. time

      • save gradients for a carefully chosen layer to let you easily recompute

3.4.4. CNNs#

  • kernel here means filter

  • convolution G- takes a windowed average of an image F with a filter H where the filter is flipped horizontally and vertically before being applied

  • G = H \(\ast\) F

    • if we do a filter with just a 1 in the middle, we get the exact same image

    • you can basically always pad with zeros as long as you keep 1 in middle

    • can use these to detect edges with small convolutions

    • can do Guassian filters

  • 1st-layer convolution typically sum over all color channels

  • 1x1 conv - still convolves over channels

  • pooling - usually max - doesn’t pool over depth

    • people trying to move away from this - larger strides in conversation layers

    • stacking small layers is generally better

  • most of memory impact is usually from activations from each layer kept around for backdrop

  • visualizations

    • layer activations (maybe average over channels)

    • visualize the weights (maybe average over channels)v

    • feed a bunch of images and keep track of which activate a neuron most

    • t-SNE embedding of images

    • occluding

  • weight matrices have special structure (Toeplitz or block Toeplitz)

  • input layer is usually centered (subtract mean over training set)

  • usually crop to fixed size (square input)

  • receptive field - input region

  • stride m - compute only every mth pixel

  • downsampling

    • max pooling - backprop error back to neuron w/ max value

    • average pooling - backprop splits error equally among input neurons

  • data augmentation - random rotations, flips, shifts, recolorings

  • siamese networks - extract features twice with same net then put layer on top

    • ex. find how similar to representations are

3.4.5. RNNs#

  • feedforward NNs have no memory so we introduce recurrent NNs

  • able to have memory

  • truncated - limit number of times you unfold

  • \(state_{new} = f(state_{old},input_t)\)

  • ex. \(h_t = tanh(W h_{t-1}+W_2 x_t)\)

  • train with backpropagation through time (unfold through time)

    • truncated backprop through time - only run every k time steps

  • error gradients vanish exponentially quickly with time lag

  • LSTMS

    • have gates for forgetting, input, output

    • easy to let hidden state flow through time, unchanged

    • gate \(\sigma\) - pointwise multiplication

      • multiply by 0 - let nothing through

      • multiply by 1 - let everything through

    • forget gate - conditionally discard previously remembered info

    • input gate - conditionally remember new info

    • output gate - conditionally output a relevant part of memory

    • GRUs - similar, merge input / forget units into a single update unit

3.4.6. graph neural networks#

  • Theoretical Foundations of Graph Neural Networks

    • inputs are graphs

    • e.g. molecule input to classification

    • e.g. traffic maps - nodes are intersections

    • invariances in CNNs: translational, neighbor pixels relate a lot more

    • simplest setup: no edges, each node \(i\) has a feature vector \(x_i\) (really a set not a graph)

      • X is a matrix where each row is a feature vector

      • note that permuting rows of X shouldn’t change anything

      • permutation invariant: \(f(PX) = f(X)\) for all permutation matrices \(P\)

        • e.g. \(\mathbf{P}_{(2,4,1,3)} \mathbf{X}=\left[\begin{array}{llll}0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\end{array}\right]\left[\begin{array}{lll}- & \mathbf{x}_{1} & - \\ - & \mathbf{x}_{2} & - \\ - & \mathbf{x}_{3} & - \\ - & \mathbf{x}_{4} & -\end{array}\right]=\left[\begin{array}{lll}- & \mathbf{x}_{2} & - \\ - & \mathbf{x}_{4} & - \\ - & \mathbf{x}_{1} & - \\ - & \mathbf{x}_{3} & -\end{array}\right]\)

        • ex. Deep Sets model (zaheer et al. ‘17): \(f(X) = \phi \left (\sum_k \psi(x_i) \right)\)

      • permutation equivariant: \(f(PX) = P f(X)\) - useful for when we want answers at the node level

    • graph: augment set of nodes with edges between them (store as an adjacency matrix)

      • permuting permutation matrix to A requires operating on both rows and cols: \(PAP^T\)

      • permutation invariance: \( f\left(\mathbf{P X}, \mathbf{P A P}^{\top}\right)=f(\mathbf{X}, \mathbf{A})\)

      • permutation equivariance: \(f\left(\mathbf{P X}, \mathbf{P A P}^{\top}\right)=\mathbf{P} f(\mathbf{X}, \mathbf{A})\)

      • can now write an equivariant function that extracts features not only of X, but also its neighbors: \(g(x_b, X_{\mathcal N_b})\)

        • tasks: node classification, graph classification, link (edge) prediction)

      • 3 flavors of GNN layers for extracting features from nodes / neighbors: simplest to most complex

        • message-passing actually passes vectors to be sent across edges

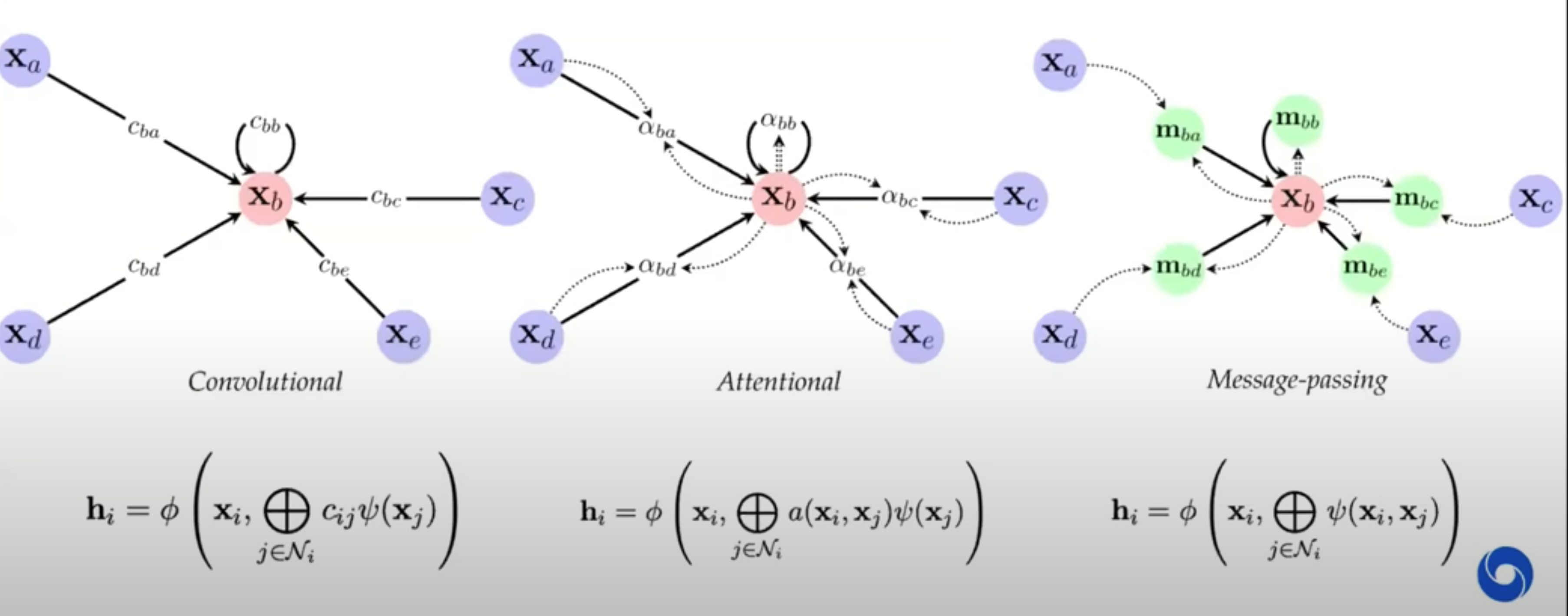
        • gnn_layers

    • previous approaches map on to gnns well

      • GNNs explicitly construct local features, much like previous works

        • local objectives: features of nodes i and j should predict existence of edge \((i, j)\)

        • random-walk objectives: features should be similar if i and j co-occur on a short random walk (e.g. deepwalk, node2vec, line)

      • similarities to NLP if we think of words as nodes and sentences as walks

        • we can think of transformers as fully-connect graph networks with attentional form of GNN layers

          • one big difference: positional embeddings often used, making the input not clearly a graph

            • these postitional embeddings often take the form of sin/cos - very similar to DFT eigenvectors of a graph

      • spectral gnns

        • operate on graph laplacian matrix \(L = D - A\) where \(D\) is degree matrix and \(A\) is adjacency matrix - more mathematically convenient

      • probabilistic modeling - e.g. assome markov random field and try to learn parameters

        • this connects well to a message-passing GNN

  • GNN limitations

    • ex. can we tell whether 2 graphs are isomorphic - often no?

    • can make GNNs more powerful by adding positional features, etc.

    • can also embed sugraphs together

    • continuous case is more difficult

  • geometric deep learning: invariances and equivariances can be applied generally to get a large calss of architectures between convolutions and graphs

3.4.7. misc architectural components#

  • coordconv - break translation equivariance by passing in i, j coords as extra filters

  • deconvolution = transposed convolution = fractionally-strided convolution - like upsampling

3.4.7.1. top-down feedback#

3.4.8. neural architecture search (NAS)#

3.4.9. misc#

Contents